Thread: The Secret Life of Chaos

This is great, chaos is my favorite. Thank you for this.

Should I get high and watch this? I think I should....

EDIT: Ok, so um....
I either misunderstood this or they explained it wrongly. I didn't end up getting high btw, so it's not that.

But basically it seems like the whole thing just said:
There are simple mathematical rules to every process.
But there are complicated mathematical rules behind those processes.

But is this really accurate?

I thought chaos theory was that there are simple mathematical rules which do explain things,
but then when you try to predict the behaviour of the thing using those rules, you can't predict it accurately.

Actually, from the show I got a little bit of both.... that you can predict it, but the maths are incredibly complicated (butterfly effect).
But they also said you can't predict it because the maths fails to work for some unknown reason.

I'm a bit tired now so I'm failing to explain coherently. Hope this makes sense.

Basically with chaos, the object you're looking at can be characterised in a simple way (e.g. z(n+1) = z(n)^2 + c for the Mandelbrot set), but when you analyse the features of the object, they are very complex. In this sense the mathematics can be both simple (a description) and complex (the analysis).

A consequence of having complex features is that for you to be able to predict anything useful, you have to know the initial variables very precisely. Think about how different one point on the border of the Mandelbrot set is from one a tiny distance from it.

Another great example is the logistic map, which was briefly shown, and I studied a bit at the start of my degree. Basically you make a model of population based on limited resources, which is in itself a huge simplification; you say that birth rate is proportional to the number of living creatures, and death rate is proportional to the square of this number (for reasons to do with limited resources). So the general formula is

next generation = r*current generation*(1 - current generation)

The thing is, even with this simplified model, the results are extremely diverse, depending on what r is (and r is deduced from the population in particular).



What this diagram shows is the stable populations for each r value. For low r, no matter what the starting population, it will soon converge to a single stable value. For r above 3, the line splits. What this means is that the population settles to a state where one year it's one value, and the next it's the other; it's oscillating. Hopefully from there you can understand the rest; the higher r, the greater the range of populations, and the greater the number of values it is oscillating between (4, then 8, then...). Pretty soon it's jumping all over the place, and then after r = 4, the population will always crash to zero.

And hopefully this shows you how we have a) a very simple equation with feedback, giving rise to b) an extremely complex object with a diversity of behaviours in a small range of values which is hence c) hard or impossible to predict.

And this is why humans should not necessarily be alarmed when the population of a species suddenly crashes for no apparent reason, and should not try to do anything about it, either. This is exactly what I mean when I say that humans show hubris when they think they can understand the world in their very simple terms and can take positive action. As is remarked in the program, we are mentally hardwired to believe that complex effects arising from simple causes is a contradiction.

The above is all just a description of chaos, though. The real message of the programme is this: we view order (pattern) and chaos as a mutually contradictory dichotomy. In reality they are both part of the same thing.

In fact if humans were naturally able to understand this, I think it's likely we'd not have felt the need to invent so many Gods to impose structure upon anarchy.

I am definetly not a mathematican nor am I very good at maths. I am fine with basics. Mathematics are interesting though. Furthermore, the concept of chaos, especially "natural chaos" is very, very interesting. I will watch the videos when I have time, thank you for the link.

Ok, so this description is closer than the other one I gave....

Originally Posted by tommo

Actually, from the show I got a little bit of both.... that you can predict it, but the maths are incredibly complicated (butterfly effect).

Still, just because the maths is complicated, I don't think that chaos can be applied to real populations so much.

I mean it probably can, but you don't need that to see why a population has crashed.
I knew this is why you think "And this is why humans should not necessarily be alarmed when the population of a species suddenly crashes for no apparent reason, and should not try to do anything about it, either. This is exactly what I mean when I say that humans show hubris when they think they can understand the world in their very simple terms and can take positive action" that.

So I tried to keep that in mind while watching, as well as basically the same argument you have for climate change.

I don't think that just because the maths becomes complicated, that we cannot find causation. We don't need to know the physics behind throwing a ball, but we can get it in to a small hoop from 20m away.

We can look at the order and see connections. We just can't do that when looking at chaos, yet. Although statistically our orderly observations will get less accurate over time.

Getting away from all that for a second....
I do understand your explanation, the population might drop because one of them steps in a hole and breaks their leg, and that hole wasn't factored in to the equation.
So why do people say that it is impossible to predict? It clearly isn't. It's just very complicated. And I think if you could find the starting point of the universe, then you could play it out in a mathematical model on the computer.
If you had the starting point accurate enough with the exact properties of all the particles etc.

I dunno, sometimes I think that a lot of mathematicians, physicists have lost connection to reality a bit. Or maybe I'm just not getting it correctly. Or maybe they just can't explain it properly.

Originally Posted by tommo

Getting away from all that for a second....
I do understand your explanation, the population might drop because one of them steps in a hole and breaks their leg, and that hole wasn't factored in to the equation.

That isn't my explanation at all, sorry if I wasn't clear. The point of the majority of the post I made was to explain this: even with an extremely simple model that doesn't take into account random events like the one you mentioned, it's still chaotic. When I described the logistic map, I did so fully: you have one very simplified term for the births per year (r*current population) and another very simplified term for the deaths per year (-r*current population^2), and even with this extremely simplified, deterministic model of a biological population, its behaviour is very complex. If you have access to some kind of simple programming language I recommend you try this for yourself... type in x = 0.5 (this is the starting population as a proportion of the maximum that the environment can support; you can choose any other number between 0 and 1), and r = 2.5 (for example). Then write x = r*x*(1-x), and repeatedly perform that operation... pretty soon x will stabilise (to 0.6). Now change the value of r. Just above 3 will give you a cycle of two populations; at 3.5 it will jump about 4 different values; then as you get close to r = 4 it will start jumping all over the place, and will be highly sensitive to the initial values of r and x.

So why do people say that it is impossible to predict? It clearly isn't. It's just very complicated. And I think if you could find the starting point of the universe, then you could play it out in a mathematical model on the computer.
If you had the starting point accurate enough with the exact properties of all the particles etc.

I dunno, sometimes I think that a lot of mathematicians, physicists have lost connection to reality a bit. Or maybe I'm just not getting it correctly. Or maybe they just can't explain it properly.

It's a popular science program, albeit quite an advanced one, so they were speaking informally to get the important message across. You are correct that if you knew literally everything to infinite accuracy about an idealised situation, you could predict everything about its future; however this is inconsequential. One of them did explain 'unpredictability' properly; no matter how accurately you know the initial configuration, it soon becomes useless. Imagine the error in your calculation multiplies by 10 each generation (so, exponential). Say your initial error is 0.0000000001, which is like knowing the circumference of the Earth to the nearest millimetre. Within only 10 generations, the error is 1 (analogous to knowing the circumference of the Earth is between zero and double what it actually is), and a few generations later it's totally useless. Now imagine we invest billions in extensive research to reduce the error by an entire factor of ten, which would be like learning the circumference of the Earth to the nearest tenth of a millimetre. How many generations does it take now before our measurement is useless? 100? Nope, it's just 11. No matter how accurately you know everything about the situation, extremely quickly it becomes completely useless, and from that point onwards you can know nothing useful at all.

To know anything useful about the future of the system after an arbitrary point would require infinite accuracy, and that is simply practically impossible. This is kinda obvious from a human perspective; we'll never be able to build instruments that are free from error. Microscopes, for instance, can only distinguish objects larger than the wavelength of light they're using. I'm not sure how serious you were about knowing absolutely everything about the start of the universe. However, all of this does in fact go beyond just human error: since the start of the 20th century, we have known that uncertainty is an inherent part of the universe; this is the uncertainty principle. Randomness is in fact a real thing, and hence chaos is intrinsic too.

Originally Posted by Xei

That isn't my explanation at all, sorry if I wasn't clear. The point of the majority of the post I made was to explain this: even with an extremely simple model that doesn't take into account random events like the one you mentioned, it's still chaotic. When I described the logistic map, I did so fully: you have one very simplified term for the births per year (r*current population) and another very simplified term for the deaths per year (-r*current population^2), and even with this extremely simplified, deterministic model of a biological population, its behaviour is very complex. If you have access to some kind of simple programming language I recommend you try this for yourself... type in x = 0.5 (this is the starting population as a proportion of the maximum that the environment can support; you can choose any other number between 0 and 1), and r = 2.5 (for example). Then write x = r*x*(1-x), and repeatedly perform that operation... pretty soon x will stabilise (to 0.6). Now change the value of r. Just above 3 will give you a cycle of two populations; at 3.5 it will jump about 4 different values; then as you get close to r = 4 it will start jumping all over the place, and will be highly sensitive to the initial values of r and x.

What does r stand for in this equation?
x is the maximum population for the environment.
nextpopulation = r*maximumpopulation*(1-maximumpopulation)
Oh wait, is it just a number representing the resources?

I'll try it in C++.

I'm not sure why that equation was chosen though.

I mean what if you just had 1+1 ?
It doesn't get more complicated.
And it is only taking in to account a few factors.
And if you had all the factors perfectly figured out (hypothetically) than the equation would not get more complicated as it goes on.

Originally Posted by Xei

It's a popular science program, albeit quite an advanced one, so they were speaking informally to get the important message across. You are correct that if you knew literally everything to infinite accuracy about an idealised situation, you could predict everything about its future; however this is inconsequential. One of them did explain 'unpredictability' properly; no matter how accurately you know the initial configuration, it soon becomes useless. Imagine the error in your calculation multiplies by 10 each generation (so, exponential). Say your initial error is 0.0000000001, which is like knowing the circumference of the Earth to the nearest millimetre. Within only 10 generations, the error is 1 (analogous to knowing the circumference of the Earth is between zero and double what it actually is), and a few generations later it's totally useless. Now imagine we invest billions in extensive research to reduce the error by an entire factor of ten, which would be like learning the circumference of the Earth to the nearest tenth of a millimetre. How many generations does it take now before our measurement is useless? 100? Nope, it's just 11. No matter how accurately you know everything about the situation, extremely quickly it becomes completely useless, and from that point onwards you can know nothing useful at all.

Ok, but what if we have computers in the future that can predict it perfectly accurately?
Especially if we have AI, it will be less prone to error than humans, or will build AI which is less prone to error.

Originally Posted by Xei

To know anything useful about the future of the system after an arbitrary point would require infinite accuracy, and that is simply practically impossible. This is kinda obvious from a human perspective; we'll never be able to build instruments that are free from error. Microscopes, for instance, can only distinguish objects larger than the wavelength of light they're using. I'm not sure how serious you were about knowing absolutely everything about the start of the universe.

Well, I'm not sure if we could figure out the start of everything.
I was just speaking theoretically. And it would probably be easier to figure out every variable at a given instant, like now, and trace it back to the beginning hehe

Originally Posted by Xei

However, all of this does in fact go beyond just human error: since the start of the 20th century, we have known that uncertainty is an inherent part of the universe; this is the uncertainty principle. Randomness is in fact a real thing, and hence chaos is intrinsic too.

Hm, I'm not so sure about this. I know quantum physics basically says this. But I think eventually we'll figure out the rules to that too. I have no proof of it or anything, I don't even really get it, but it's just what I think.

The equation is just a simple model of a simple circumstance in nature, and is chosen because it's illustrative of the general principle of chaos in nature, and in systems with feedback. The equation is deduced logically... for example, it is obvious if you think about it that birth rates are proportional to the population, if uninhibited. r is just a constant representing proportionality, it is nothing intuitive.

AI has nothing to do with this. Error does not mean 'whoops I spilled acid in the fish tank'; it is a technical term meaning uncertainty. All scientific apparatus has a degree of error associated with it. You can only use a ruler to an accuracy of about half a millimetre, so any value you give must be quantified as 'x millimetres plus or minus 0.5 millimetres'; a range of values. You can't reduce this range to zero, because technology is not infinitely powerful; it is limited by physics. The lenses in your microscopes are made of atoms and can't form perfect shapes, for instance; and due to their temperature they will be jiggling around, etcetera.

The equations are pure but extremely fine grained abstractions; the problem is with the data.

We will never find out any useful information about what lies behind quantum phenomena (even if there were a reason to think there is anything 'behind' it), because what the law is telling us in the first place is that you won't ever be able to measure it. The uncertainty principle is a precise equation with a precise number which is determined by the universe and is an inherent part of it.

If there were zero randomness in the universe, after the Big Bang everything would simply have expanded into a homogeneous mass; but it definitely didn't do that. Recognise this?



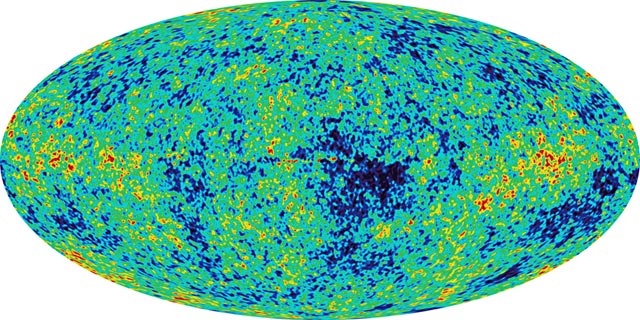
It's the cosmic microwave background. You can roughly view this as representing the start of the universe. The red blotches are a little bit hotter than the blue ones, because of 'quantum fluctuations'; tiny little deviations in temperature. This meant that certain parts of the universe were denser than others; this in turn caused galaxies, stars, and planets to form, and thus life. A tiny difference in the tiny volume before the Big Bang would have meant the entire universe would be a completely different shape, with totally different galaxies. This is a great example of chaos.

Originally Posted by Xei

The equation is just a simple model of a simple circumstance in nature, and is chosen because it's illustrative of the general principle of chaos in nature, and in systems with feedback. The equation is deduced logically... for example, it is obvious if you think about it that birth rates are proportional to the population, if uninhibited. r is just a constant representing proportionality, it is nothing intuitive.

Ok this is a little off topic, but I've seen this basically exact thing mentioned before (on a chemistry video).
He said that x was just a constant. What does that actually mean in maths?
Like why can you just have any constant? And why does it not have to be defined?

Originally Posted by Xei

AI has nothing to do with this. Error does not mean 'whoops I spilled acid in the fish tank'; it is a technical term meaning uncertainty. All scientific apparatus has a degree of error associated with it. You can only use a ruler to an accuracy of about half a millimetre, so any value you give must be quantified as 'x millimetres plus or minus 0.5 millimetres'; a range of values. You can't reduce this range to zero, because technology is not infinitely powerful; it is limited by physics. The lenses in your microscopes are made of atoms and can't form perfect shapes, for instance; and due to their temperature they will be jiggling around, etcetera.

The equations are pure but extremely fine grained abstractions; the problem is with the data.

lol okay, but if our equipment is as sensitive as it can possibly be.
Actually, don't worry about this. I understand what you're saying and if I take it further, we're just getting in to unknowns about the future and what we could do.
So yep I understood what you meant by that.

Originally Posted by Xei

We will never find out any useful information about what lies behind quantum phenomena (even if there were a reason to think there is anything 'behind' it), because what the law is telling us in the first place is that you won't ever be able to measure it. The uncertainty principle is a precise equation with a precise number which is determined by the universe and is an inherent part of it.

Well how can you be so certain that we will never know the rules behind it?
As you said, nothing is exact, certain or completely accurate.

Originally Posted by Xei

If there were zero randomness in the universe, after the Big Bang everything would simply have expanded into a homogeneous mass; but it definitely didn't do that. Recognise this?



It's the cosmic microwave background. You can roughly view this as representing the start of the universe. The red blotches are a little bit hotter than the blue ones, because of 'quantum fluctuations'; tiny little deviations in temperature. This meant that certain parts of the universe were denser than others; this in turn caused galaxies, stars, and planets to form, and thus life. A tiny difference in the tiny volume before the Big Bang would have meant the entire universe would be a completely different shape, with totally different galaxies. This is a great example of chaos.

I don't think that's a good example tbh.
We don't even know if our universe is the first one.
As an illustration of the point it is a good example though.
But if our universe came through a black hole or something, it would have had other forces from that universe making it non uniform.

But even so, if it was just the usual big bang theory, the particles that were created would interact with each other, would they not? (even just gravity, not collisions or anything) Which would create the illusion of randomness.

This is an interesting subject! As a non-mathematician, calling it chaos gives me a huge headache. From what I can see it's not "chaos" so much as, a complexity that we humans can't predict! When I look at this type of math, I feel like I'm really looking at something so much more. Like theres layers and layers of truth being revealed. It makes me think of time, life, free will.

Off Topic Rant:
But this statement is really annoying

"It's a mindbending, counterintuitive and for many people a deeply troubling idea. But Professor Al-Khalili reveals the science behind much of beauty and structure in the natural world and discovers that far from it being magic or an act of God, it is in fact an intrinsic part of the laws of physics. Amazingly, it turns out that the mathematics of chaos can explain how and why the universe creates exquisite order and pattern."

Only those who believe in God can say what their God does or does not do, not the other way around. Neither chaos, order, or any intrinsic natural law necessarily go against the belief of God. Depending on who you are, such an intrinsic natural property of the Universe is absolute evidence that there is no God, or its absolute evidence that there is! In short, its not the place of science or math to start a religious or spiritual war.

Science programs should just ignore religion altogether.
I hate it when they feel the need to put in some religious reference at the end.

That's why I like David Attenborough documentaries, coz he never mentions it.
Unless it has to do with something that is being explained, like how priests found the Galapagos and thought it was hell on Earth.

Awesome, I actually watched this a few times early last year, I love all of Jim Al-Khalili's programs and books. This was actually one of my first posts on this forum on a thread concerning order and chaos "Maybe reality is really like order and chaos fused as one, we only separate them in our heads." It's very inspiring to see that science and mathematics are getting closer and closer to describing the true nature of this self-sufficing universe. I'm still a little fuzzy on what chaos could be besides our lack of precision or quantum uncertainty, but that and whether there is an underlying reason why uncertainty is inherent in quantum physics are definitely interesting things to think more about.