I find this fascinating. I'm especially amazed by fractals, there's something very profound about them. |
|
Results 1 to 3 of 3
Thread: Rolling Hypocycloids
-
12-12-2013 09:28 PM #1
 Rolling Hypocycloids
Rolling Hypocycloids
Link from which I transferred: Rolling Hypocycloids
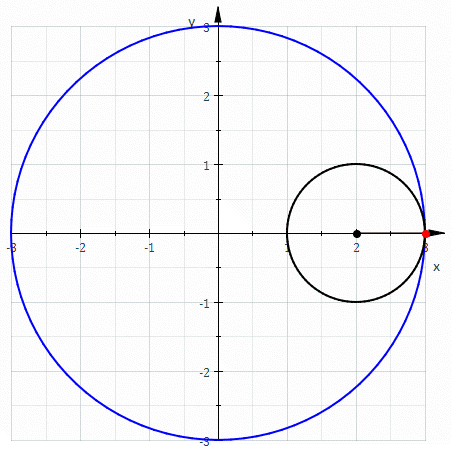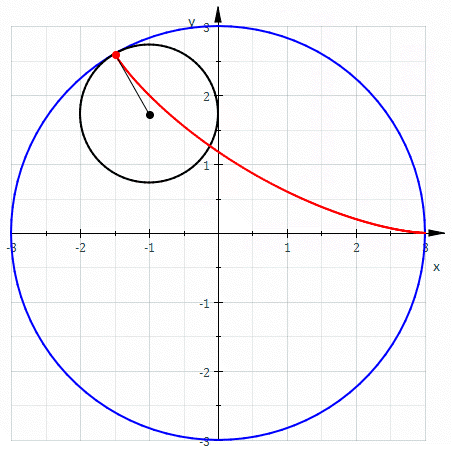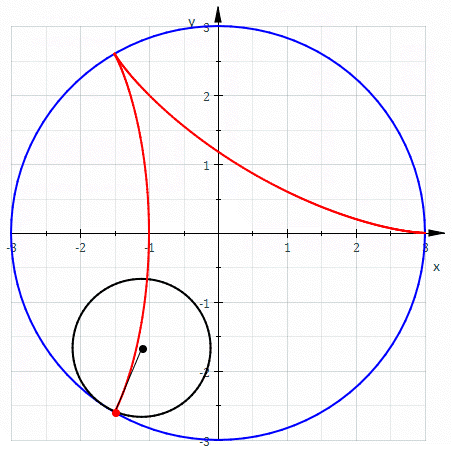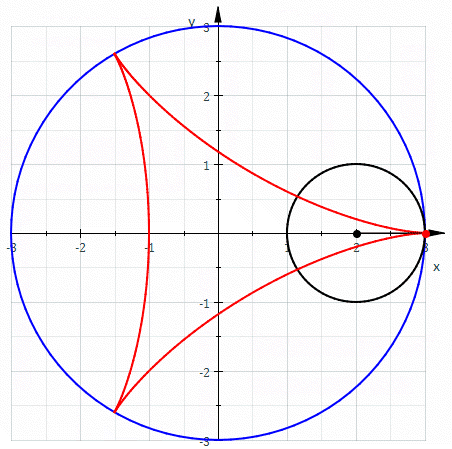
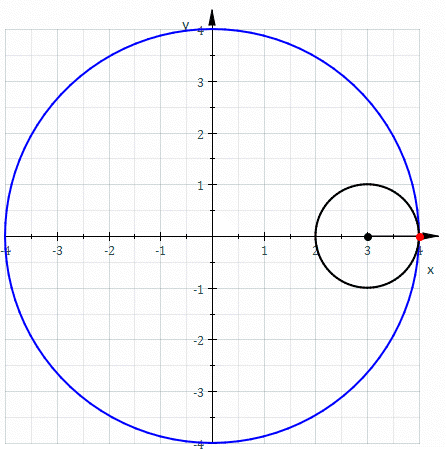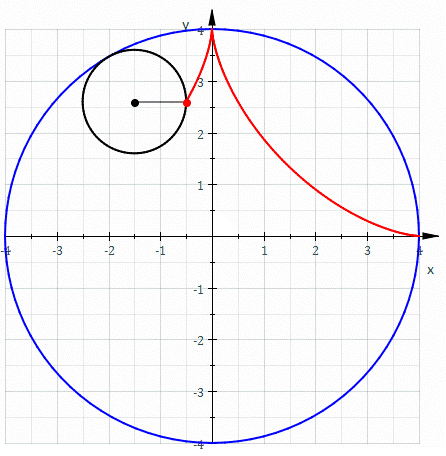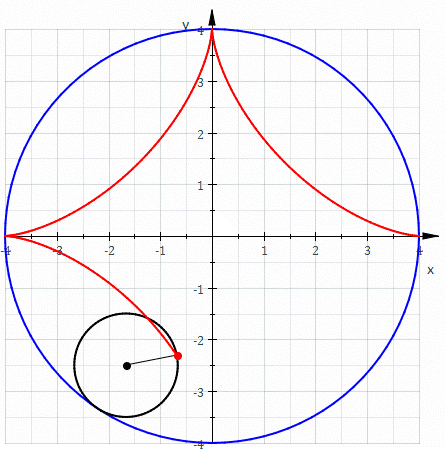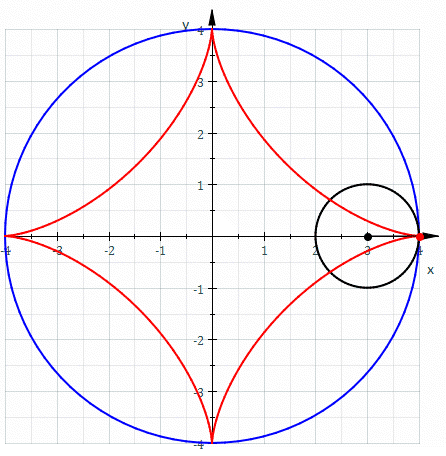
The hypocycloid with n cusps is the curve traced out by a point on a circle rolling inside a circle whose radius is n times larger.
The hypocycloid with 2 cusps is sort of strange:
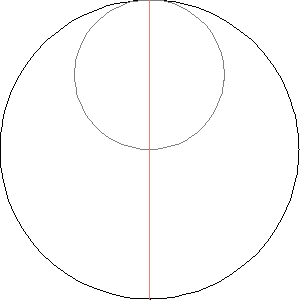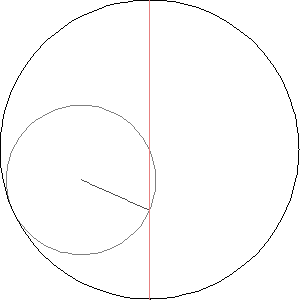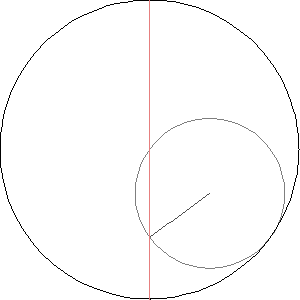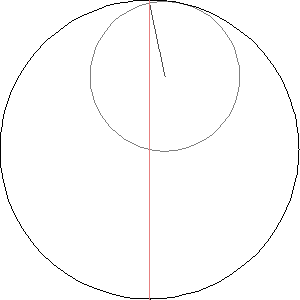
It’s just a line segment! It’s called the Tusi couple.
The hypocycloid with 3 cusps is called the deltoid, because it’s shaped like the Greek letter Δ:
The hypocycloid with 4 cusps is called the astroid, because it reminds people of a star:
I got interested in hypocycloids while writing some articles here:
- Rolling circles and balls.
My goal was to explain a paper John Huerta and I wrote about the truly amazing things that happen when you roll a ball on a ball 3 times as big. But I got into some interesting digressions.
While pondering hypocycloids in the ensuing discussion, the mathematician, physicist, programmer and science fiction author Greg Egan created this intriguing movie:
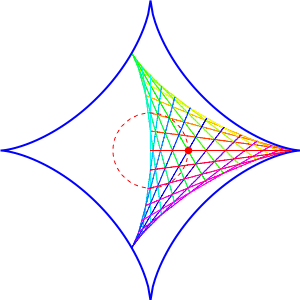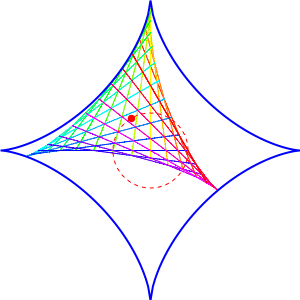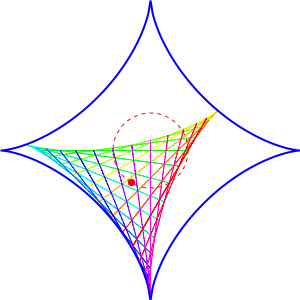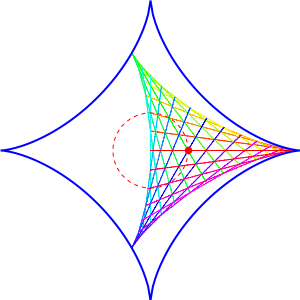
It’s a deltoid rolling inside an astroid. It fits in a perfectly snug way, with all three corners touching the astroid at all times!
Why does it work? It’s related to some things that physicists like: SU(3) and SU(4).
SU(n) is the group of n × n unitary matrices with determinant 1. Physicists like Pauli and Heisenberg got interested in SU(2) when they realized it describes the rotational symmetries of an electron. You need it to understand the spin of an electron. Later, Gell-Mann got interested in SU(3) because he thought it described the symmetries of quarks. He won a Nobel prize for predicting a new particle based on this theory, which was then discovered.
We now know that SU(3) does describe symmetries of quarks, but not in the way Gell-Mann thought. It turns out that quarks come in 3 ‘colors’—not real colors, but jokingly called red, green and blue. Similarly, electrons come in 2 different spin states, called up and down. Matrices in SU(3) can change the color of a quark, just as matrices in SU(2) can switch an electron’s spin from up to down, or some mix of up and down.
SU(4) would be important in physics if quarks came in 4 colors. In fact there’s a theory saying they do, with electrons and neutrinos being examples of quarks in their 4th color state! It’s called the Pati–Salam theory, and you can see an explanation here:
• John Baez and John Huerta, The algebra of grand unified theories.
It’s a lot of fun, because it unifies leptons (particles like electrons and neutrinos) and quarks. There’s even a chance that it’s true. But it’s not very popular these days, because it has some problems. It predicts that protons decay, which we haven’t seen happen yet.
Anyway, the math of SU(3) and SU(4) is perfectly well understood regardless of their applications to physics. And here’s the cool part:
If you take a matrix in SU(3) and add up its diagonal entries, you can get any number in the complex plane that lies inside a deltoid. If you take a matrix in SU(4) and add up its diagonal entries, you can get any number in the complex plane that lies inside an astroid. And using how SU(3) fits inside SU(4), you can show that a deltoid moves snugly inside an astroid!
The deltoid looks like it’s rolling, hence the title of this article. But Egan pointed out that it’s not truly ‘roll’ in the sense of mechanics—it slides a bit as it rolls.
For the details, see this article on my other blog:
• Deltoid rolling on an astroid.
But the really cool part—the new thing I want to show you today—is that this pattern continues!
For example, an astroid moves snugly inside a 5-pointed shape, thanks to how SU(4) sits inside SU(5). Here’s a movie of that, again made by Greg Egan:
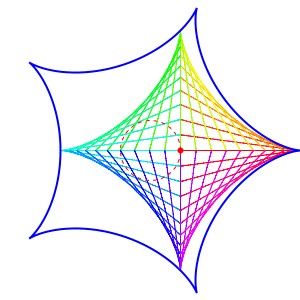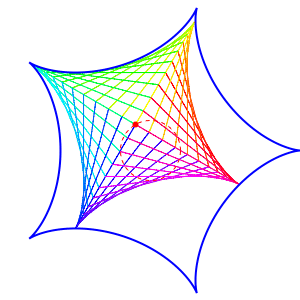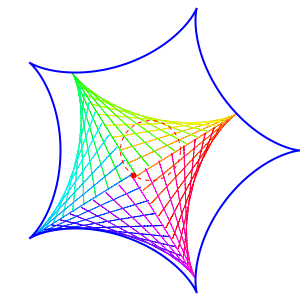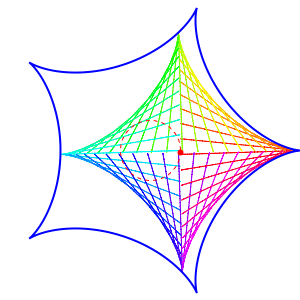
In general, a hypocycloid with n cusps moves snugly inside a hypocycloid with n + 1 cusps. But this implies that you can have a hypocycloid with 2 cusps moves inside one with 3 cusps moving inside one with 4 cusps, etcetera! I’ve been wanting to see this for a while, but yesterday Egan created some movies showing this:
Depending on the details, you can get different patterns:
Egan explains:
In the first movie, every n-cusped hypocycloid moves inside the enclosing (n+1)-cusped hypocycloid at the same angular velocity and in the same direction, relative to the enclosing one … which is itself rotating, except for the very largest one. So the cumulative rotational velocity is highest for the line, lower for the deltoid, lower still for the astroid, in equal steps until you hit zero for the outermost hypocycloid.
In the second movie, the magnitude of the relative angular velocity is always the same between each hypocycloid and the one that encloses it, but the direction alternates as you go up each level.
Here’s one where he went up to a hypocycloid with 10 cusps:
Note how sometimes all the cusps meet!
Yonatan Zunger is the chief architect of Google+, but before that he used to work on string theory. Reading about this stuff on Google+, he had a number of interesting ideas, like this:
I wonder, can a deltoid roll in a 5-hypocycloid? I haven’t worked through the math of just how the SU(n) → SU(n+1) embedding guarantees a fit here.
(And also, are there corresponding pictures we could draw to illustrate the embeddings of other Lie groups? This could be a lovely way to illustrate a wide range of relationships if it could be done more generally.)
Egan figured out that yes, a deltoid can move nicely in a hypocycloid with 5 cusps:
He writes:
To make this, I took the border of a deltoid in “standard position” (as per the trace theorem) to be:
\mathrm{deltoid}(t) = 2 \exp(i t) + \exp(-2 i t)
Suppose I apply the linear function:
f(s, z) = \exp(-2 i s / 5) z + 2 \exp(3 i s / 5)
to the whole deltoid. Then at the point s=t on the deltoid, we have:
f(s, \mathrm{deltoid}(s)) = 4 \exp(3 i s / 5) + \exp(-4 (3 i s / 5))
which is a point on a 5-cusped hypocycloid in “standard position”. Of course with this choice of parameters you need to take s from 0 through to 10 \pi/3, not 2 \pi, to complete a cycle.
Using the same trick, you can get a hypocyloid with n cusps to move inside one with m cusps whenever n ≤ m. As for the more general question of how different Lie groups give different ‘generalized hypocycloids’, and how fitting one Lie group in another lets you roll one generalized hypocycloid in another, the current state of the art is here:
• N. Kaiser, Mean eigenvalues for simple, simply connected, compact Lie groups.
But there is still more left to do!
On a somewhat related note, check out this fractal obtained by rolling a circle inside a circle 4 times as big that’s rolling in a circle 4 times as big… and so on: astroidae ad infinitum!
Go click the link for the last animations, which are missing in the above - and the links, I just transferred as text!
I did not attempt to understand much further than "what physicists like"- but I find it interesting and beautiful as far as I get just now!
Enjoy!Last edited by StephL; 12-12-2013 at 09:33 PM. Reason: fiddling..
-
12-13-2013 12:08 AM #2
-
12-13-2013 12:51 PM #3
Ah - niice - somebody likes it!!
Actually it was so: I sent a link to the amplitudihedron next door to my husband - who is a mathematician. But he works in internet-security informatics - not the "real deal".
He started a conversation with a physicist about it per mail - to properly understand it and the implications - and came out quite exhilarated.
I said - sorry - no stop it - I mainly like how it looks and that something beautiful and geometrical is actually useful for figuring out "quantum-stuff". Ähäm..
But on the other hand - I really love watching/listening to enthused scientists - and enthused mathematicians can be even better.
So - in the end I got this as a mail from him - for my enjoyment, mainly..
And fractals are indeed very profound - they make up the optical side of chaos-theory, which is a whole new branch of mathematics.
I might open a thread on Benoit Mandelbrot as well - who came up with them.
There is a marvellous youtube series from Arthur C. Clarke on the whole topic - where Mandelbrot comes to word also - but unfortunately he is dead by now.
If I remember correctly - they had this super simple formula for the Mandelbrot set - and a not very fast computer - but when the black and white roughly rendered thing came out - they had made a new step in mathematics - nobody had seen this before - I think it was the 80s - and they were blown away by the beauty of what they had found.
Since there are tons of also optical consequences from it - up to the patterns on big cat´s fur and convection in fluids and all sorts of beautiful things - I tried to venture into it a bit myself - but I gave up after a rather short while.
At the end of my patience - but maybe not my wits - I lent a wonderful book, I got myself - big format - many many pictures - but everything explained - with formulas - some special edition of Scientific American - to another mathematician friend of mine.
The plan was to have her read it and then explain to me..
I´m afraid she has other stuff on her mind just now - but I wanted to call her anyway - good reminder this.
Similar Threads
-
rolling wilds
By vector1327 in forum Wake Initiated Lucid Dreams (WILD)Replies: 3Last Post: 09-03-2009, 08:37 PM -
Rolling over
By Souperman22 in forum Attaining LucidityReplies: 2Last Post: 07-10-2009, 10:46 PM -
Rolling out
By Ghaerdon in forum General Lucid DiscussionReplies: 3Last Post: 05-04-2008, 01:52 PM -
Rolling out of bed?
By Predator-S in forum General Lucid DiscussionReplies: 7Last Post: 01-07-2008, 01:11 AM -
Rolling rolling rolling
By Maystar in forum Dream Journal ArchiveReplies: 0Last Post: 12-08-2004, 06:06 PM




 5Likes
5Likes LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks







 Reply With Quote
Reply With Quote


Bookmarks