0 doesn't go into 1 at all, that's why we say it's 'undefined'. If 0 went into 1 X times where X is any well defined entity then 1/0 would be defined (as X). |
|
Results 1 to 25 of 83
-
03-24-2012 08:13 AM #1
1/0
Division by zero (1 divided by 0) is undefined instead of being 0 because 0 can divide 1 infinitely many times. But that seems rather odd because the number 1 displays countable properties (ie. 1 glass of water, or 1 piece of toast) whereas 0 quantifies a count of null size. In other words, 0 cannot go into 1 infinitely many times when it hasn't gone into 1 at all.
Thoughts?
-
03-24-2012 11:53 AM #2Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
-
03-24-2012 12:06 PM #3
who actually cares
-
03-24-2012 12:11 PM #4Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Having interests?

THAT'S LAME MUM.
-
03-24-2012 06:24 PM #5
Here's an annoying maths thing someone told me. Xei will see right through it instantly obviously, but hey, it confused me a lot.
So i=sqrt(-1),
-1=1/-1
Sqrt(-1)=sqrt(1/-1)=sqrt(1)/sqrt(-1)
=1/i=-i
Resulting in i=-i
What's wrong?
Made me want to tear my hair out.
-
03-24-2012 07:27 PM #6Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Another version would be -1 = i*i = sqrt(-1)*sqrt(-1) = sqrt(-1*-1) = sqrt(1) = 1.
Something similar is
i^i = [exp(i*pi/2)]^i = exp[(i*pi/2)*i] = exp(-pi/2) (which = 0.207879576 roughly, it's pretty cool that i^i is just a real number).
But also i^i = [exp(i*5pi/2)]^i = exp[(i*5pi/2)*i] = exp(-5pi/2).
In fact i^i = exp(-npi/2) for any integer n of the form n = 4m + 1.
These things are quite an annoyance really, and the basic answer as to why it's wrong is just 'you're not allowed to do that'. But what you can do is define multivalued functions where all of the answers are correct. The square root function which is at the centre of your problem gives + and - something, and gives you graphs which look kinda like this:
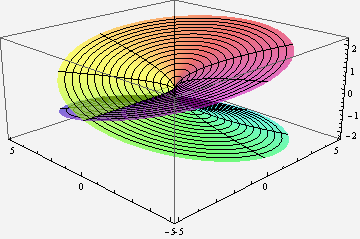
The log function on the other hand which was at the centre of my problem can be represented by something like this:
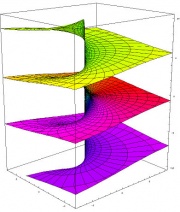
-
03-24-2012 07:32 PM #7
Awesome...
Yeah, I was kinda pissed off when the answer to the problem turned out to be 'i=1,-1' because I had spent about an hour going insane over it...
EDIT of course, I actually meant sqrt(-1)=i, -iLast edited by Patrick; 03-24-2012 at 10:36 PM.
-
03-24-2012 07:36 PM #8
Wow, I was about to start a thread on this general issue. It is really trippy. I have seen several variations, but this is the one I have been getting opinions on in the last few days.
-1 = -1
1/-1 = -1/1
sqrt (1/-1) = sqrt (-1/1)
sqrt 1 / sqrt -1 = sqrt -1 / sqrt 1
1/i = i/1
i(1/i) = i(i/1)
1 = i^2
1 = -1
I think the resolution is related to the paradox involved in squaring i. There is a conflict of rules. One rule in math is that if you multiply the square root of x by the square root of y, you get the square root of xy. Another rule is that when you square a square root, you get the number you were getting the square root of. So what happens when you square the square root of -1?
sqrt -1 X sqrt -1 = sqrt (-1 X -1) = sqrt 1 = 1
or...
(sqrt -1)^2 = -1
Which is it? If you call sqrt -1 "i," the rule is that you get -1. The other rule seems to pose a problem, and that results in the crazy "proofs."
I have taught advanced algebra, yet I still sneer at imaginary numbers. They are hypotheticals that the math community admits involve an absurd premise. I think the "proof" is a reductio ad absurdum of imaginary numbers. They are bullshit. There is no square root of -1. They are called "imaginary numbers" for a reason.You are dreaming right now.
-
03-24-2012 08:17 PM #9Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
There is no contradiction. It is simply that the proof that sqrt(xy) = sqrt(x)sqrt(y) only works if x and y are non-negative integers; it is not a general 'rule of math' for all entities x and y. Write out the proof and see.
I suppose I'm part of the 'mathematical community', so let me allay some misconceptions. Imaginary numbers do not involve an 'absurd premise'. They are just as concrete as any other real number, like 0, -1, or sqrt(2). All they are is arrows, which add in the obvious way, and multiply by scaling and rotating. In fact you can construct them using only the real numbers, addition, multiplication, and ordered pairs. If you grant that these things are well defined, you are compelled to grant that complex numbers are just as well defined. It's very simple to do: you define complex numbers as the set of ordered pairs of real numbers (a,b), with two operations,
(a,b) + (c,d) = (a + c, b + d)
(a,b)*(c,d) = (ad - bc, ad + bc)
You say you've taught advanced algebra, so it should be easy for you to check that this construction satisfies the conditions of a field. Also check that numbers of the form (a,0) form a subfield, and that there is an isomorphism from this subfield to the field of real numbers under the normal addition and multiplication operations. Finally, check that (0,1)*(0,1) = (-1,0).
That's all complex numbers are. Nothing more, nothing less. 'Imaginary number' does not mean a hypothetical number any more than 'complex number' means a complicated number or 'irrational number' means an absurd number. All of these names are historical artefacts.
They are also extremely useful. You can even use them to prove things about real numbers that are hard otherwise. For instance, you can use properties of the complex integers ((a,b) where a and b are integers) to classify all numbers which are the sum of two squares. The answer turns out to be all those numbers which don't have a prime factor of odd power with remainder 3 after division by 4.
-
03-24-2012 08:37 PM #10
The proof you want me to check out involves imaginary numbers, so the proof involves an absurd premise. I know that a lot of the rules of math can be applied to imaginary numbers and the results are logical from the standpoint that there is such thing as the square root of -1. The premise is still absurd. You can use a lot of logical hypotheticals using Santa Claus also, but they are still based on an imaginary premise.
Irrational numbers are real. They just involve the impossibility of writing them as an integer divided by an integer. I know that the word "irrational" can mean "illogical," but that is not the context of the word as it applies to numbers. It means basically "non-ratio-able." What is the reason behind the term "imaginary numbers?" Complex numbers involve imaginary numbers, but the coeffient of i can be 0. In such a case, the value is real, so there is no problem there.
The rule you discussed about the product of the square roots of x and y does not include imaginary numbers because they are... imaginary. Something eventually goes wrong when a piece of the puzzle is illogical.
I am not quite sure what you were trying to say in the last sentence.You are dreaming right now.
-
03-24-2012 08:57 PM #11Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
No... the proof involves non-negative reals. The point is that if they aren't, it doesn't have to go through: there is no requirement that the result should be true for complex numbers, and thus there is no contradiction: the issue is resolved. The same would apply to other things that you are presumably happy with, such as matrices; sqrt(A)sqrt(B) = sqrt(AB) doesn't hold for them either, and for the same reason.
You haven't specified what the premise is that you are talking about. I just posted the formal construction of the complex numbers: you need to point out where the problem is.I know that a lot of the rules of math can be applied to imaginary numbers and the results are logical from the standpoint that there is such thing as the square root of -1. The premise is still absurd. You can use a lot of logical hypotheticals using Santa Claus also, but they are still based on an imaginary premise.
Like I said, it is a historical hangover. 400 years ago they didn't have a formal construction of the complex numbers, so they made the same mistake as you in thinking that there was something ill-defined about them.Irrational numbers are real. They just involve the impossibility of writing them as an integer divided by an integer. I know that the word "irrational" can mean "illogical," but that is not the context of the word as it applies to numbers. It means basically "non-ratio-able." What is the reason behind the term "imaginary numbers?" Complex numbers involve imaginary numbers, but the coeffient of i can be 0. In such a case, the value is real, so there is no problem there.
The basic point is that imaginary numbers are a consistent structure and they are extremely useful for all kinds of real-world problems, including non-complex number theory. By refusing to use them you severely hinder your ability to obtain answers to various problems, from differential equations to diophantine equations.I am not quite sure what you were trying to say in the last sentence.Last edited by Xei; 03-24-2012 at 09:03 PM.
-
03-24-2012 09:05 PM #12
Jeez UM, you really hate complex numbers for no reason...
-
03-24-2012 10:13 PM #13Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
It's an understandable mistake and one that was historically widespread... I believe British mathematics after Newton was quite hindered by it, much more progress was made on the continent where they were much faster to accept complex numbers for what they were.
I think the root of the problem can be expressed in this way: we get our concept of number from abstraction from various physical instances. For instance, whole numbers such as the number 3 come from the perceived commonality between three fish and three rocks and three trees, and the consistent way in which this abstraction behaves. Addition and multiplication are similarly sourced. This is all very fine, but there are two pitfalls.
Firstly, you can assign some kind of special ontological status to the number: you may be so impressed by the abstraction that you say that the number 3 is 'real'. Whether this is correct naturally depends on what you define 'real' to mean; if you mean a specific, solid entity, then clearly the number 3 is not real, and neither is the number i, for that matter. If, however, you mean an abstraction that behaves in a consistent manner, then the number 3 is real, and so is the number i.
And secondly, you can identify that which is abstracted from with the abstraction itself, and end up with too narrow a definition. For instance, you may make the mistake of saying that multiplication of n by m just is the number of things you have when you have n lots of m things (fish, rocks, trees). Of course, this becomes very problematic when you come across irrational numbers, and you may, like the Pythagoreans, reject 'the number that multiplies by itself to give 2', as a 'hypothetical' or an 'absurdity'. The correct approach, as we now know, is simply to accommodate such entities into your abstraction; as long as it's still consistent. Not only does this give you a much richer theory with the potential to provide new truths about your simpler abstraction: it also turns out that there is a correct 'grounding' to abstract from; namely lengths (the diagonal of a unit square being the 'hypothetical' number). If you view multiplication in the aforementioned non-abstract way, you will reject i, that is, 'the number which multiplies by itself to -1', as something which is patently not 'real'. And in the very limited scope to which you have confined yourself, you are effectively correct; no grouping of groupings of physical objects will give you -1. But again, if we simply accommodate i, we again get a consistent system which is much more powerful than the old one, even in the old one's domain. And again, it actually turns out that a more general grounding, namely that of two dimensional arrows, encapsulates your abstraction.
-
03-24-2012 10:34 PM #14Banned


- Join Date
- Jun 2008
- Location
- N/A
- Posts
- 354
- Likes
- 177
-
03-25-2012 12:00 AM #15
^ Yeah, that insight was very well explained. I'm actually doing a metaphysics paper on this right now. I'm also interested to see what physical phenomena or properties can be described by complex numbers and why.
-
03-25-2012 12:06 AM #16
I must have misunderstood what proof you are talking about. Could you post it? Like I said, there can be a large amount of consistency in hypotheticals with absurd premises, though when taken to the nth degree, inconsistency can be shown somewhere. Movies about the paranormal don't have to have contradictions, for example, but they are based on absurd principles. The rule about multiplying square roots of negatives is such an inconsistency.
What do you think is the resolution to the "proof" I posted? Is it too basically just a "you're not allowed to do that"? The rules have to be made up when you are dealing with things that do not fit into reality.
The premise that -1 has a square root. It's made up.
If that were the case, the terminology would need to change. Words like "real" and "imaginary" mean things. i does not exist in nature. It is a man made construct.
Like I said, the disappearance of the rule that a product of square roots equals the square root of the product of the radicands shows an inconsistency. However, I do recognize that they can be used for figuring things out, just like political and legal hypotheticals can be used for figuring things out. It does not make them real, though.
Your next post went way into that issue, and I agree with a lot of it. However, I think i is very different from negative numbers and the square root of 2. The square root of 2 is irrational, but it is still a real quantity, as is pi. Pi is the ratio of the circumference of a circle to its diameter. (I know you already knew that. I just said it so it can be taken into account.) That is an actual quantity, a number of things. You can't have -3 rocks, but you can be -3 feet in front of a starting line by being 3 feet in front of it or owe somebody -3 dollars if the person owes you 3 dollars. It is a measure of the tangible reality of you having given the person 3 $1 bills. Imaginary numbers don't fit into reality like that. They just make useful hypotheticals. There can't be i of anything.
So, it's not purely about physical tangibility or consistency. It's about quantifiability as it relates to the tangible.
Ha ha, what? I don't hate them. I think they're fascinating, as I said about the "proofs" we've been discussing. I love this stuff. I don't believe in the Flying Spaghetti Monster either, but it's an interesting concept.
We atheists tend to mention the FSM in every debate about whether something exists. He too is a very useful hypothetical.You are dreaming right now.
-
03-25-2012 12:19 AM #17
To add a little to the original topic, zero is tricky because it has the property that for any x, 0 *x = 0. So dividing through by zero (pretend we're allowed to), we get x = 0/0. So we can divide zero into zero and get anything.
Now suppose that 1/0 = x. Then 1 = 0*x. But this is absurd.
That's the reason it's undefined. It makes no sense. We can't even say how many times zero "goes into" zero let alone one.Previously PhilosopherStoned
-
03-25-2012 12:23 AM #18
Isn't the premise that 1 exists made up too?
The square root of 1 is 1. This just makes finding the square root of -1 a problem of signs. -1 and 1 share the absolue value of 1, and this seems to me like it could make sign somewhat insignificant in describing nature, and really just make the sqrt(-1) a problem with formalism. The creation of i then wouldn't seem any less "real" in describing nature if this is true, just a way for the formalism to get where it needs to go.Last edited by Wayfaerer; 03-25-2012 at 12:29 AM.
-
03-25-2012 01:15 AM #19Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
I'm sorry UM but you are not following the conversation; I can only recommend that you reread. I already responded to your supposed contradiction (which I had also posted beforehand), that's what this whole bit of the conversation was about in the first place. To recapitulate: there is no contradiction because sqrt(a)sqrt(b) is not sqrt(ab) in general, only when a and b are non-negative reals. There is no issue of 'making rules up', the proof works for non-negative reals and it doesn't work in general; these things come from the axioms.Like I said, the disappearance of the rule that a product of square roots equals the square root of the product of the radicands shows an inconsistency.
I don't know how there's any ambiguity in which proof I'm referring to. We are talking about sqrt(a)sqrt(b) = sqrt(ab) for a, b non-negative. The proof of this fact is therefore the one I am talking about; I recommend you try to prove it and examine every step very carefully to see how general it is. The failure of this identity for numbers other than a, b non-negative does not somehow show that complex numbers are inconsistent any more than the failure of the identity for matrices shows the inconsistency of matrices, or the failure of 1/tan@ = cos@/sin@ for @ = 0 shows the inconsistency of 0.
These terms are all undefined. Please define exactly what you mean by 'it's made up'. In particular you need to explain how this differs from the premise that 2 has a square root is made up. Refer very carefully to my latest post which is about this exact issue.The premise that -1 has a square root. It's made up.
Ditto.If that were the case, the terminology would need to change. Words like "real" and "imaginary" mean things. i does not exist in nature. It is a man made construct.
Yes, this is all covered in that post. There can't 'be i of anything', but by your own admission there can't 'be -3 of anything' either. Different numbers have different contexts; a context for negative numbers is displacements, like you said, rather than quantification of numbers of objects. A context for pi or sqrt2 are lengths. Put a mug on the floor in front of you. Now turn it around by 90 degrees anticlockwise. You have just multiplied that mug by i. Turn it by 180. You've just multiplied it by i^2. That's a good context for imaginary numbers. Rotating a mug certainly seems to me to be just as 'quantifiable as it relates to the tangible' as the circumference of the mug or the number of mugs.Your next post went way into that issue, and I agree with a lot of it. However, I think i is very different from negative numbers and the square root of 2. The square root of 2 is irrational, but it is still a real quantity, as is pi. Pi is the ratio of the circumference of a circle to its diameter. (I know you already knew that. I just said it so it can be taken into account.) That is an actual quantity, a number of things. You can't have -3 rocks, but you can be -3 feet in front of a starting line by being 3 feet in front of it or owe somebody -3 dollars if the person owes you 3 dollars. It is a measure of the tangible reality of you having given the person 3 $1 bills. Imaginary numbers don't fit into reality like that. They just make useful hypotheticals. There can't be i of anything.
So, it's not purely about physical tangibility or consistency. It's about quantifiability as it relates to the tangible.
-
03-25-2012 01:16 AM #20
That's another interesting way to look at it. I have always taught Xei's explanation, but I like your equation too.
0 cannot be multiplied by any number to get a number other than itself, but 0 can be multiplied by any number to get itself. So, a non-zero number divided by 0 is no number, but 0 divided by itself is all numbers (so to speak in a bizarre way), so it is no particular number exclusively. I think 0/0 is what caused the big bang.
No. Look at one $1 bill.
I agree that it is a problem of signs, but the signs have realistic meanings, and they make all the difference. What number can you multiply by itself to get -1 or any other negative number? A negative times a negative is a positive, and a positive times a positive is a positive. The square root of 0 is 0. A number squared to get a negative number would not be positive, negative, or 0. What is it? It's not real.You are dreaming right now.
-
03-25-2012 01:19 AM #21Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
-
03-25-2012 01:19 AM #22
Xei, you should definitely become a professor. This is the first time someone has been trying to explain maths to me and I've actually understood it!
-
03-25-2012 01:40 AM #23Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
I'm certain I'd be fairly miserable as a maths professor... I have been strongly considering doing part time private tuition though, especially for gifted kids who need some intellectual stimulation beyond the dismal mire of the UK curriculum.

That sounds really interesting, care to elaborate?
Of relevance, a very edifying question for me is, 'if two different models predict the same observed phenomena, to what extent can they be said to be correct'?
Complex numbers are actually pretty ubiquitous in applied math... even in things like differential equations (solving the motion of a pendulum for instance) are greatly helped by them.
The really interesting one of course is quantum mechanics. Feynman and others say that complex numbers are effectively indispensable to the formulation of the theory.
This raises the very interesting question of how we discovered the language of the universe many centuries before by the totally unrelated and prosaic act of trying to solve cubic equations.Last edited by Xei; 03-25-2012 at 01:48 AM.
-
03-25-2012 01:42 AM #24
-
03-25-2012 02:18 AM #25
Didn't you get my pm a while back?
 I'm basically trying to find out how true new empiricism/psychologism is as the foundation of mathematics. Philosophy of mathematics - Wikipedia, the free encyclopedia
I'm basically trying to find out how true new empiricism/psychologism is as the foundation of mathematics. Philosophy of mathematics - Wikipedia, the free encyclopedia
If both are consistent with all observed phenomena then I guess you couldn't really say until new observations or a better model shows up.
Quantum mechanics is such a conceptual mess right now that I don't think anything could be rightly called it's true "language" yet. We can do with what we have and I suppose something we made before was bound to be the best one to describe such unfamiliar things. Why they work could hide something profound, we just won't know until we make more sense of everything.




 17Likes
17Likes LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks



 Reply With Quote
Reply With Quote



Bookmarks