It's easier with fractions. Note that sin(pi/2) = 1, and sin(0) = 0. |
|
Results 1 to 25 of 38
Thread: Maths question lul
-
12-24-2011 11:47 AM #1Finding the way... Achievements:









- Join Date
- Jan 2011
- Gender

- Location
- England
- Posts
- 1,573
- Likes
- 414
- DJ Entries
- 63
Maths question lul
Why is 0.25sin^4(0.5pie) - 0.25sin^4(0) = 0.25 :S
-
12-24-2011 01:55 PM #2
Last edited by Dianeva; 12-24-2011 at 01:57 PM.
-
12-24-2011 03:53 PM #3Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah... because if you input the values for sin that's what you get, lul.
-
12-24-2011 05:00 PM #4
I'm stuck on a maths question as well. Might as well just post it here to get an answer.
Find the general solution of the differential equation: tan(x)(dy/dx) +y = e^(2x)*tanx
I found that the integrating factor is e^(1/tanx) = e^(lnsinx) = sinx
Multiplying every term by sinx:
sinx (dy/dx) + y (sinx/tanx) = e^(2x)*sinx
But now when I do integration by parts it just goes in a loop..Last edited by ThePieMan; 12-24-2011 at 06:36 PM.
-
12-24-2011 05:56 PM #5Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Check out the homework guideline sticky...
If you've studied DEs I don't see why you shouldn't be able to do that. What's your specific confusion?
-
12-24-2011 06:51 PM #6Finding the way... Achievements:









- Join Date
- Jan 2011
- Gender

- Location
- England
- Posts
- 1,573
- Likes
- 414
- DJ Entries
- 63
Flaw in my math knowledge soz, didnt realise that sin^4 is the same as the 0.5pie^4 if that makes sense.
-
12-24-2011 10:59 PM #7
-
12-25-2011 12:29 AM #8Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
You'll be trying to integrate 1/tanx, yesh?
Write down the definition of tan. You should be able to integrate by substitution.
-
12-25-2011 12:59 AM #9
sinx (dy/dx) + y (sinx/tanx) = e^(2x)*sinx
=>I started by using some basic trig sinx/tanx = sinx/(sinx/cosx) = cosx
=>So now the equation looks like: sinx y'' + ycosx = e^(2x)*sinx
I then tried to do integration by parts by letting u = e^(2x) , u'=2e^(2x) , v = -cosx , v' = sinx
Was this the wrong step to take?Last edited by ThePieMan; 12-25-2011 at 01:02 AM.
-
12-25-2011 01:07 AM #10Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah, to use that method you first have to get it into the form y' + fy = g; in other words, divide the whole thing by sinx.
-
12-25-2011 01:27 AM #11
Oh I see. Thanks man

-
12-25-2011 01:32 AM #12
Out of curiosity, what subjects did you take before university? Further maths I presume?
-
12-25-2011 01:48 AM #13Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah, and phys, chem, bio. They're not very demanding. The only exam I had to spend a long time training for was STEP, although the syllabus is just maths and further maths.
-
12-25-2011 02:10 AM #14
Wow that's impressive. I wouldn't be able to cope with that many subjects.
And how is it that you don't find further maths demanding?!
-
12-25-2011 02:19 AM #15Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Meh I found it to just be learning set methods. I don't think there's much conceptually hard stuff... they just give you a list of different things you have to be able to do, and the set of instructions you follow to do them. There's no thinking involved, just memorisation of a list of things. Science A-Levels are exactly the same, it gets boring once you get used to it.
Check out some of these which have the same syllabus as A-Level but the opposite emphasis:
STEP Test Preparation | University Admissions Tests from Cambridge Assessment
I had to pass II and III.
-
12-25-2011 06:49 PM #16
That stuff looks intimidating... But I suppose it ought to be if its the admissions test to one of the best universities in the world.
Now I know who to ask when I'm stuck on a question
Last edited by ThePieMan; 12-25-2011 at 06:52 PM.
-
01-31-2012 10:07 PM #17
A mechanics problem:
A particle is projected from a point P on an inclined plane, up the line of greatest slope through P, with initial speed V. The angle of the plane to the horizontal is θ.
(i) If the plane is smooth, and the particle travels for a time 2Vcosθ/g before coming instantaneously to rest, show that θ=pi/4
(ii) If the same plane is given a roughened surface, with a coefficient of friction 0.5, find the distance travelled before the particle comes to rest.
---
I managed to do (i) by considering the components of gravity on an inclined plane, then using v=u+at. V, g terms cancel and you get θ=pi/4.
Not sure how to do part (ii)...
Help is appreciated.
-
01-31-2012 10:31 PM #18Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
The key with pretty much all of those mechanics modules is just to draw a diagram... it's basically the same deal in this question, except you have a frictional force. I can't really remember how those things work, but isn't it just that a frictional force of mu times the reaction force of the surface opposes the motion?
In this case it's pretty much the same question as before, except you have to work out the reaction force (which is done in pretty much the same way as you found the decelerating component of the weight), and add that to the deceleration. Then it's just equations of motion again.
-
01-31-2012 10:40 PM #19
I'm guessing you'd have to find the mass, right? Then maybe use the work-energy theorem?
-
01-31-2012 10:52 PM #20
Hmm not quite - I think the correct approach is to actually consider the components of gravity (gsinθ, gcosθ etc), but I have no idea how to deduce the reaction force from that..
-
01-31-2012 10:57 PM #21
I just figured the coefficient of friction wouldn't be of use without knowledge of the normal force on the particle.
Last edited by Wayfaerer; 01-31-2012 at 11:00 PM.
-
01-31-2012 11:07 PM #22
Meh I'll try to solve it at some later date. I'll be sure to post detailed solutions to satiate your curiosity.

-
01-31-2012 11:25 PM #23
Sounds good, I could probably find it helpful to post some of my own homework problems here later

-
01-31-2012 11:34 PM #24
Cool. You might see some complex number problems here in the near future.
-
02-01-2012 12:32 AM #25Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Bro I answered your question lol...
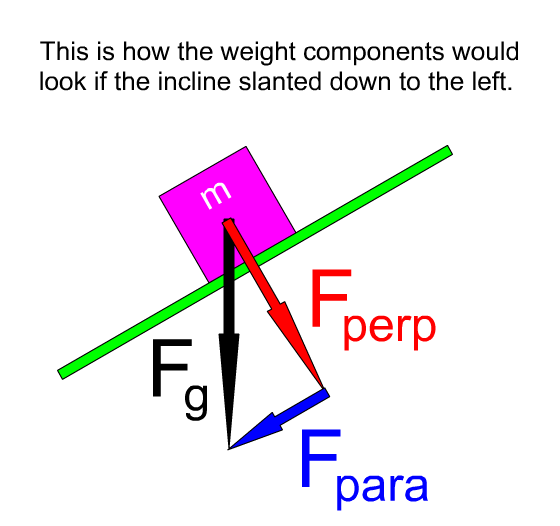
Random helpful image from Google. The green line makes an angle @ with the horizontal by definition, and also by simple geometry the red and black lines also make an angle @. Fg is just the weight force of the particle, and from that you can calculate Fperp which is the reaction force just like you calculated Fpara which is the retarding gravitational component.
Similar Threads
-
Maths and Hallucinations
By nina in forum Science & MathematicsReplies: 13Last Post: 06-02-2012, 01:00 AM -
Maths before sleep produce vivid lucid dreams?
By Flywithme in forum Introduction ZoneReplies: 5Last Post: 03-24-2011, 12:26 AM -
Fancy Maths Stuff!
By Xei in forum Science & MathematicsReplies: 37Last Post: 03-10-2011, 07:42 PM -
Maths!
By wendylove in forum Science & MathematicsReplies: 11Last Post: 04-22-2009, 07:24 PM -
Maths says that we're nearing the end of human life!
By Xei in forum Extended DiscussionReplies: 14Last Post: 07-16-2007, 07:05 PM




 LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks





 Reply With Quote
Reply With Quote

Bookmarks