I don't see why not. Infinity is essentially comprised of everything. Positive and negative numbers, which it goes in both direction. A lot of people just view infinity as going in one direction with a line of positive number. |
|
Results 1 to 25 of 29
Thread: Different kinds of infinity?
-
07-18-2010 10:38 AM #1
Different kinds of infinity?
I recently watched a documentary that introduced the Continuum Hypothesis (nothing in depth at all) and George Cantor, the famous mathematician. They discussed the notion of different kinds of infinities, but didn't get into the details or explanations. I assume this is because this aired on public television, and the technicalities would go over the heads of... everyone. I don't expect I'd understand right off the bat either.
In any case, the video described a circle in a new way to me. A circle was superimposed on the screen, and the narrator would draw a triangle, a square, and so on inscribed within the circle, and then went on to explain that a circle was essentially a shape with an infinite number of angles if all of the side and angles were the same. After thinking about it for a moment however it also occurred to me that circles have perfect curves, and no sides as can be distinguished be being separate from one another by any angle. A circle has infinite angles, but it also has zero angles? Is something like that theoretically possible? Cantor went insane and was put into an asylum several times over the course of his attempts to prove the Continuum hypothesis. The documentary touched upon contradictory elements in his work.. Again though, there isn't much in terms of specifics.
To conclude: I want to know more about different kinds of infinity, and whether or not infinity can be equal to zero in some cases.
PS- I found the documentary on page 65 of the Abstruse Goose webcomic, aptly titled, "The Cantor Madness."
PPS- I have some understanding of countable and uncountable number sets.Last edited by Invader; 07-18-2010 at 10:41 AM.
-
07-18-2010 05:25 PM #2Member

- Join Date
- Mar 2010
- Location
- Where ever
- Posts
- 365
- Likes
- 28
Last edited by ArcanumNoctis; 07-18-2010 at 06:15 PM.
-
07-18-2010 06:13 PM #3Member

- Join Date
- Mar 2010
- Location
- Where ever
- Posts
- 365
- Likes
- 28
Just just watched a video of someone breaking down the theory.
The Infinities In Between (1 of 2)
The Infinities In Between (2 of 2)
-
07-19-2010 05:48 AM #4Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
I absolutely love this kind of mathematics, it's my favourite stuff we've covered in my degree so far (which is strange because I'm not normally a fan of pure maths).
I didn't think that Cantor was crazy per se, but I do know that he suffered depression later in life because almost everybody else rejected his work as rubbish. Another mathematician at the time told him it was about 100 years to early for mathematicians to handle, which turned out to be pretty much true.
Basically, infinity is usually used to mean one of two completely distinct concepts.
First there is the infinity of analysis (which concerns itself with limits). An example of its usage would be
'As x tends to 0, 1/x^2 tends to infinity'.
Colloquially this is easy to see
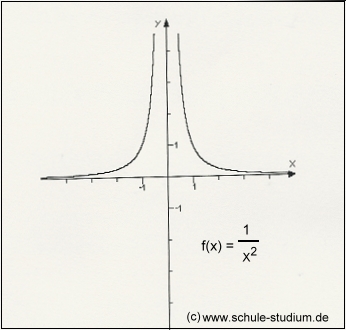
but the colloquial interpretation is actually completely wrong, because in this context infinity is not a number; it's totally wrong to think of infinity as some huge thing arbitrarily high up the y axis which the function is heading towards.
In symbolic terms what 'as x tends to a, f(x) tends to infinity' actually means is this beastie:
∀ ε > 0 ∃ δ > 0 : |x - a| < δ ⇒ f(x) > ε
which in English means 'no matter how high a number you give me, I can give you a range of values around a so that the function is higher than your number'.
In other words, in analysis, infinity only really has meaning when it is used as a part of other expressions, and never means a value, but rather some kind of process (in this case unbounded increase).
In number theory however, which is what Cantor was concerned with, infinity has a totally different meaning. It's much more like a number than the infinity of analysis in the sense that it's kind of used for counting objects, but it's a bit more subtle than that.
Basically when we count things, we are pairing them off with elements of the set of natural numbers ('N'), which are
1, 2, 3, 4, ...
If you were counting 3 sheep for example, you pair sheep 1 with 1, sheep 2 with 2, sheep 3 with 3, and then you have no more sheep to pair up, so your number of sheep is 3.
When things get really interesting is when you try to count infinite sets.
An easy example to start with is the set {0, 1, 2, 3...}. Can we count this? Using the above, this question is equivalent to 'can we pair up every element in this set with an element in N?'.
It's quite easy to see how (N is on the left):
1 - 0
2 - 1
3 - 2
4 - 3
...
We can be confident with this set up that every element in N is going to be paired up with an element in our set, and importantly, that no elements in our set are going to be left out.
Therefore, we say, our set has the same size as N, which we call 'Aleph-0'.
Surprisingly we can also do this with the rational numbers ('Q'), which is the set of all fractions. We do this in the following way:

Again, we've assigned every fraction a number in N, and we can be sure that we've 'hit' every fraction, hence the size of the set of fractions is Aleph-0.
Now we try for the reals ('R'), which are colloquially the 'decimals'. This set is called the 'continuum' because there is a sort of smoothness about it; it forms a line with no gaps (unlike the naturals or rationals; for example the square root of 2, or pi, will be gaps in both of these sets).
Imagine that we've done it and we've got some system of pairing up, e.g.
1 - 1.1200394810...
2 - 0.0013223491...
3 - 2.2221340139...
4 - 1.0104910495...
The trick now is to construct some decimal which differs from the decimal paired to 1 in the first digit, the decimal paired to 2 in the second, and so on. We do this by changing 0s to 1s and everything else to 0s. In this case we will get:
0.101...
This is called the diagonal slash method. As our decimal differs from the nth listed decimal by the nth digit, we know that our list will always miss it. Hence, there are 'more' real numbers than natural numbers, and we have different 'sizes of infinity', which are denoted by different aleph numbers.
The continuum hypothesis is simply that the size of the real numbers is Aleph-1, or the 'next infinity up' from the naturals' Aleph-0, i.e. there are no sets with more elements than N but less than R.
This turns out to be impossible to decide with the normal rules of mathematics. What mathematicians have to do, then, if they require it for a proof, is simply accept it is true or accept it is false (and yes, this often gives mutually contradictory results). This is related to Godel's incompleteness theorem. It's not really unhealthy though, because with all mathematics you have to start with some base assumptions (or 'axioms'), for example 'a(b + c) = ab + ac' is no more provable than the continuum hypothesis, and must be assumed for all that follows.
Regarding the circle question: that seems to be a question relating to the infinity of analysis rather than Cantor's infinities, because it's regarding an unbounded limiting process (rather than counting things).
You are right that it is impossible to have an infinite number of angles which don't exist, and this touches on a point which is crucial to the whole of analysis: there is a distinction between the limit as you approach something, and the value when you actually hit it. If there were not, analysis would be redundant.
Take for example the previous function 1/x^2; the limit as x tends to 0 clearly exists, but there is no value AT x = 0.
In the same way a circle is the limit of the process you described, but the nonexistence of the object at the 'end point' of the process (which is of course a contradiction because the process is infinite) does not matter.
I think that covers most of the basic ideas... a good idea might be to try to count some of the following:
Z = {..., -2, -1, 0, 1, 2, ...}, the integers.
N^2 = {(a,b) such that a and b are in N}, the set of all pairs of numbers.
Q^2 = {(a,b) such that a and b are in Q}, the set of all pairs of fractions.
{non-overlapping discs in a plane}; picture a dalmatian with circular spots. Remember there could be infinitely many spots (the dalmatian is grotesquely obese).
{non-intersecting figures of 8}; this is hard but awesome.
{set of all subsets of N}
No, he wasn't. He was heavy into proper mathematics. Sacred geometry is a load of nonsense. It doesn't even mean anything.It sounds like the guy was heavy into sacred geometry.
-
07-19-2010 06:40 PM #5Member

- Join Date
- Mar 2010
- Location
- Where ever
- Posts
- 365
- Likes
- 28
Last edited by ArcanumNoctis; 07-19-2010 at 06:44 PM.
-
07-19-2010 09:23 PM #6
-
07-19-2010 11:33 PM #7Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yes, good point there.
Sacred geometry makes no predictions, uses no logical inference, in fact has no logical meaning whatsoever. It is literally a bunch of pretty pictures with pretty names with no explanation whatsoever. Anybody could make up such a thing.
-
07-21-2010 04:03 PM #8Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
I'd like to see how many of those sets people can count...
They're roughly in difficultly order, though perhaps the last two should be swapped. Most of them are linked to the previous one.
Z = {..., -2, -1, 0, 1, 2, ...}, the integers.
N^2 = {(a,b) such that a and b are in N}, the set of all pairs of numbers.
Q^2 = {(a,b) such that a and b are in Q}, the set of all pairs of fractions.
{non-overlapping discs in a plane}; picture a dalmatian with circular spots. Remember there could be infinitely many spots (the dalmatian is grotesquely obese).
{non-intersecting figures of 8}; this is hard but awesome.
{set of all subsets of N}
-
08-12-2010 08:12 PM #9
∞ ≠ ∞
That's a little something I learned in Calculus during infinite series.
infinity.jpg
This is where infinity gets fun.Last edited by The Invisible Man; 08-12-2010 at 08:13 PM. Reason: Stupid attachment editor

Can you see me now?
-
08-12-2010 09:02 PM #10
-
08-12-2010 11:04 PM #11Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Give us the quick lowdown on how you did the first three.

The next two are slightly more abstract. Basically with the first one (for example), you're on the infinite 2D plane (like a normal coordinate system) and circles of random sizes are dotted all over it in random positions. There could be a finite number or an infinite number (although if there were a finite number it's obvious they're countable), and you have to find some way of counting them; in other words, in pairing them up with the natural numbers so that no circle is unpaired.
A big clue for all of the first five is that they all follow from the previous one.
You're correct that the last one is bigger than N, though of course the point is in proving it. The clue here is to try to adopt the method that was used for proving the real numbers are uncountable.
Well... infinity doesn't equal infinity because it isn't a number. Though using it informally there shouldn't really be a problem in equating them. A ≠ A can never make any sense if A is well defined.
Dunno what's going on with the sum... I don't think it makes any sense. If you mean the sum from 1 to infinity... I don't really know why the ns haven't been cancelled. I think 1/n^2 sums to pi^2 / 6.
-
08-13-2010 01:12 AM #12
I haven't totally been able to wrap my head around this. Non-overlapping discs in a plane is a bunch of visual objects that are distinguished from one another by the space in between them. We designate a number to each one. 1 assigned to this spot, 2 assigned to that spot, and so on for infinite (if there are an infinite number of spots). That doesn't mean that any spot has a value of 1 or 2 or n, the number only signifies the amount of spots. Is that correct?
And two questions:
What do you mean by intersecting figures of eight?
What designation of Aleph do we give to a number set that includes all numbers, like the set N such that N goes from -∞ to +∞ where an infinite number of numbers exists between any two numbers (as in there are an infinite number of irrational and non irrational numbers in between 1 and 2, or between 4.0005 and 4.0005001)?
Also, your explanations have been helpful and I thank you profusely for them.
-
08-13-2010 02:57 AM #13Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah, that's correct. It's just slightly contentious whether we can actually do this. You're right that intuitively it seems clear that we can just slap a number on random circles, but mathematically we'd require a proof that this can actually be done in a rigorous manner without leaving any circles out. I mean, it seems kinda intuitive that we can just 'slap a number' on random decimals, but this actually turns out to be mistaken.
As an example of where you might not be entirely certain you can count them: say you have three circles just touching (not intersecting) each other, forming a 'triangle'. Then you put a circle in the hole in the middle that just fits. Then you put even smaller circles in the new holes. Then you repeat this an infinite number of times, so you get something a bit like the Apollonian gasket:
http://upload.wikimedia.org/wikipedi...ian_gasket.svg
How exactly would you order these circles from 1 to infinity, making sure every single circle gets included?
And what if this pattern was repeated an infinite number of times at regular spaces all over the plane?
Hopefully you see why it's not so clear that all of these circles could be counted.
I repeat my advice to illidian which is that each question was designed to follow from the previous.
Another good, related thing to count would be non-intersecting circles rather than discs (circles are just the line bit (hollow), discs are 'solid'. So, for example, you can have circles within circles). The answer is that they're uncountable, but to show this I again repeat my advice to illidian; try to find a way to make this analogous to showing the reals are uncountable.
In case you didn't see, the question is about non-intersecting figures. Intersecting figures of eight are clearly uncountable because you could put the middle of each figure of eight on every real number on the x axis.And two questions:
What do you mean by intersecting figures of eight?
Basically, by figure of eight I mean any shape which consists of two loops joined together at a single point. The shape of the loops doesn't matter (they could be massive squiggles). By non-intersecting, I mean if you have two figures of eight, they can't 'cross over' each other. The figures of eight aren't solid though; you can put a figure of eight inside the loop of another figure of eight.
The answer to this one is really cool. Basically you need to ask what is unique to each figure of eight, in order to count it.
Technically those sets don't include 'all numbers' ('number' is kinda vague... you can have numbers with multiple dimensions etc.), but I know what you mean; you're talking about sections of the real number line.What designation of Aleph do we give to a number set that includes all numbers, like the set N such that N goes from -∞ to +∞ where an infinite number of numbers exists between any two numbers (as in there are an infinite number of irrational and non irrational numbers in between 1 and 2, or between 4.0005 and 4.0005001)?
Also, your explanations have been helpful and I thank you profusely for them.
The answer is Aleph-1 (if the continuum hypothesis is correct; if not, just whatever the cardinality of the real numbers is). So any section of the real number line contains the same number of numbers as any other section, or indeed the entire number line, which is kind of amazing. This further shows why it's called 'the continuum'; it's stretchy. You can take any section of the reals and 'stretch it up' and shift it about to any other arbitrarily large section without losing any of the fidelity.
For example, you can set up a one-to-one correspondence (called a 'bijection' in maths; I might have mentioned that already. Showing a set is countable is equivalent to finding a bijection between the set and the natural numbers) between [0, 1] and [0, 2], with a simple function:
f(x) = 2x.
This sends 0 to 0, 0.5 to 1, 1 to 2, and so on for all the numbers inbetween.
We can also biject [0, 1] (say) to [0, ∞] with the function:
f(x) = 1/x.
It's quite easy to see why these sets are all the same size if you look at the original proof. In the proof I gave, I could have continued giving numbers between 0 and 10. Or, quite easily, I could have used the diagonal slash argument on numbers between 0 and 1. It really doesn't matter. I only needed to prove that a small section of the real numbers were uncountable to prove that the totality of the real numbers were uncountable.
Hope that helps.Last edited by Xei; 08-13-2010 at 03:02 AM.
-
08-13-2010 09:21 AM #14
Oh, ok. I wasn't sure if it's ok to post the solution already.

Here's how I did the first three (not sure if they're correct though):
Counting Z:
z : N → Z and
z(1) = 0
z(2) = 1
z(3) = -1
z(4) = 2
z(5) = -2
z(6) = 3
z(7) = -3
etc.
Counting N^2:
n : N → N^2 and
n(1) = (1,1)
n(2) = (1,2)
n(3) = (2,1)
n(4) = (1,3)
n(5) = (2,2)
n(6) = (3,1)
n(7) = (1,4)
n(8) = (2,3)
n(9) = (3,2)
n(10) = (4,1)
etc.
Counting Q^2:
Let q : N → Q be the function that counts Q,
let n : N → N^2 be the fuction that counts N^2
and f : N^2 → Q^2 with f( (x,y) ) = (q(x), q(y)).
Then q2 : N → Q^2 with q(x) = f(n(x)) would count Q^2.
Now I got to think about the other ones.
-
08-13-2010 01:04 PM #15Banned

- Join Date
- Nov 2007
- Gender

- Posts
- 1,674
- Likes
- 200
View of the Two-Element metaphysics.
Definition: A thing is any material difference in any shape, form, limit.
I.e. shape is not a thing. material difference is not a thing.
One cannot predicate of either material or form, they are first principles, elements.
One cannot define either matieral difference or form, for the above reason.
Definition is the social convention which preserves the naming convention which equates the names of a thing to the names of that things various forms and material differences in those forms. I.e. predication is the inverse function of abstraction.
Description is a set of directions leading to a thing by which an abstraction of either material difference or form may be made.
One can use the above principles of logic to determine that a great deal of Cantor's work was insane and that the questions you have asked, most are basically non-linguistic--not in compliance with the principles of grammar at all.
If one does not know the foundation of langauge, they do not know when they are thinking gibberish or not, they have no standard by which to understand that words, just like arthithmetic, has principles by which words can be assembled into basic sentences, basic sentences into the complex sentences we use now.
It is an effect long ago noticed, but ignored. This effect is also a major theme in the Judeo-Christian Scripture and that one day, a point in history would be made signaling a psychological change in man--because it is a linguistic change. Man is still proto-linguistic.
Example: "Set of all numbers".
A number is no more than a name derived from an order naming convention.
Thus one has "Set of all names." Is the material in a boundary the boundary which bounds itself?
Can one have the set of all names? How does that effect relation to self? If you do not understand, what is the name of the set of all names? The liars paradox in another form. A set is a thing, the material in a set is not, in reference to the set. One cannot have a thing of a not thing. All of man's so call higher logics and math are gibberish. Plato's Parmenides was suppose to exercise the mind to demonstrate what happens when one uses the same name for a thing, a things form, and the material difference in that form. The principles of predication.
Demonstration: If I say a set of marbles. "a set" is a variable, one can substitute "house", A house of marbles.
A house made of marbles, to clarify. Which is not really good grammar, we should say a house made with marbles.
Without understanding we do not even know when to use "of" or "with".
Once more: There is a difference between "naming" which produces "names" and the "names" produced.
Naming is a material difference--i.e. it is not a thing. Names, if language were at all possible, must be set in a one-to-one correspondece with that which is named. A name can have NO characteristics of its own in order for it to be logically manipulated as that which is named. Which means, there is no common characteristic of a name qua name by which to even construct a set. Now, if you have studied grammar as taught today, you will quickly realize that what you are taught is contradictory to language itself.Last edited by Philosopher8659; 08-13-2010 at 02:55 PM.
-
08-13-2010 09:19 PM #16Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah, perfect. I kind of left a clue for the second one with the picture for counting the rationals. You did pretty much the same thing it looks like... the trick of course is counting them diagonally; if you count them horizontally or vertically you'll never get past the first line. And yeah, with the third you just gotta realise that you can combine the previous functions.
Are you in education at the mo? You could probably handle maths at Cambridge, especially if you manage the next questions.
-
08-13-2010 10:13 PM #17
Yeah, I'm a university student, studying Software Engineering.
So, here's my idea for counting non-overlapping discs in a plane.
I've already shown that one can count Q^2. So I have an (infinite) list of all pairs of rational numbers. I go down that list, interpret each pair as coordinates on the plane, and check if the point described by the coordinates is in one of the discs. If I get a hit, I assign the next number to that disc – I'm starting at 1, of course.
The only thing I'm not sure about is how would I know if I've hit a disc. In what form are the discs given. I assume they're just given visually (somehow). If they were in a some sort of a list I would already have a way to count them, wouldn't I. I'm probably thinking too much like a programmer here.

-
08-13-2010 10:54 PM #18Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Yeah, that's pretty much perfect. :V
I dunno about your question about what form they're in... in maths we'd think of a collection of discs as a well-defined objective entity. You could think of them as a set of coordinates of centres paired with radii or something, but we'd view that as a description really, rather than the actual object itself.
A couple of subtleties about the answer; firstly each disc is actually counted an infinite number of times. Of course, that's not actually a problem. If you show that each disc can be mapped onto N an infinite number of times you can obviously do it a single time.
Secondly the proof relies on what we call the 'density of the rationals'. What this means is that, between any two non-equal values, you can find a rational number. This is necessary for the subtle step that you actually can find a point in Q^2 inside the disc; if the question were about points, it wouldn't work.
-
08-14-2010 07:40 AM #19
Maybe I am looking at this too much from a practical standpoint, but I still want to explain what bugs me about this. If the discs are given as a well-defined set and I want to check if a given point is in one of the discs, I imagine I would start looking through the set, trying to find a disc that contains my point. If there was such a disc, I would eventually find it (in finite time). If there wasn't, however, I would look for it forever and I wouldn't be able to count that set, i.e. not all discs would eventually get a number assigned to it because I would be stuck trying to find a disc for a point that is not contained in any disc.
I also just realised that, to be consistent, I would have to raise the same issue for the counting of Z (or N^2, Q, or Q^2).
I find this all a little confusing. It almost seems like a philosophical issue. Maybe all I have to do is imagine how such a bijection would look like, but I'm a little sceptical of proofs that I am unable to express formaly. How would you show that the set of non-overlapping discs (let's call it D) is countable in a rigorously formal way? Such a proof should have the following basic structure:
1. Explicitly give a function f : N → D.
2. Formally show that f is injective, i.e. show that f(a) = f(b) → a = b.
3. Formally show that f is surjective, i.e. show that ∀d∈D: ∃n∈N: f(n) = d.
I imagine that you could do that for Z and probably for Q, N^2, and Q^2, too, but I am unsure how this could be achieved with D.
I think the difference between Z and D is that for Z, even though it is an infinite set, I have a finite description. For D I don't have a finite description, do I? But if I don't have a finite description of D, there is no practical way to check if a given point is in any of discs. You said that D is given as a "well-defined set". Does "well-defined" imply that the definition (= description) is finite? If the definition was finite, I imagine it would be possible to check if a given point is in any of discs. If the definition was not finite, I can't really imagine how it would be done.
-
08-14-2010 11:54 PM #20
I had a room mate that raised a similar objection to Cantors work. His exact words: "Stick N in one bucket and R in another and start pulling one item out of each bucket. When one bucket runs out, you know the other one is bigger."
The problem with this is that it's not a computational thing.
think of there being a set S = {n in N: there exists d in D s.t. f(n) in d} where f is the chosen bijection N -> Q2. We don't need to actually construct this set to work with it.We just need to know that it's well defined. Essentially, you can think of a set S as being well defined if for every element e in the universe of discourse, either e is or is not in S. An example of set lacking well-definition. The canonical example of this is the set A of all sets which are not members of themselves. Is A a member of itself or isn't it?
So S defined above is well-defined if d is a well defined set for all d in D and if D is well defined which we'll assume for now. but we can just represent d as the set d = {(x, y) : sqrt((x - c1) + (y - c2)) < r), where c is the center of the disc and r is the radius. This is clearly well defined. Then proving that card(D) = card(N) is equivalent to proving that the map S -> d in D induced by S is surjective.* This is technically trivial but may or may not be challenging for an intelligent person that's not used to this sort of stuff. Technically, we would have to prove a surjection of D onto N as well but in this case, I think were safe to assume that one exists.
* this is the map θ: N -> D, that takes n to the disc that contains f(n). This is defined for every element of S by construction. To see that it is well-defined, note that if f(n) lies in d1 and d2 then d1 intersect d2 is non-trivial contradicting our assumptions on D.Last edited by PhilosopherStoned; 08-15-2010 at 09:53 AM.
Previously PhilosopherStoned
-
08-15-2010 07:28 AM #21
-
08-15-2010 09:45 AM #22
xei left the definition of D open because we can just assume that it's well defined and a particular definition of it just obscures the issue. If some particular D happens to lack well-definition, then the proof doesn't apply to that D. I'll give you an example though. For simplicity of notation that's define D(x, r) as the disc of radius r centered at x.
D = {D(x, 1/2): for all x with positive integer coordinates}
If we take this D, then the proof is utterly trivial, because we can just apply the same argument that you used to prove the denumerability of N2.
D = {D(x, 1): for x = (r, θ) with r = eθ and θ in N}
This one is super trivial.
I'm not really in the mood too cook up an esoteric example, but those are two definitions that yield well defined sets. They also illustrate the value of assuming that something you want is well defined: it lets you construct general proofs. with either of those sets, the particular proof is trivial.
As for as for your question about well-definition requiring a finite definition, I don't know how to answer that because I don't know what an infinite definition would look like. Both of the examples above 'yield' an infinite set.
You mention that you're a computer programmer. If you've done any functional programming (and CS profs love love love functional languages) then you are probably familiar with the filter function. think of a set definition like the filter function. I toss stuff into it and if it passes through the definition, then it's part of the set.
I also reread my last post and am going to edit it a bit to make it clearer and fix one ugly typo.Last edited by PhilosopherStoned; 08-15-2010 at 09:54 AM.
Previously PhilosopherStoned
-
08-15-2010 02:24 PM #23
I see now. I guess the problem was my insufficient grasp of the concept of well-definition, as well as my bringing abstract notions like infinite definitions into the discussions (I meant a definition that takes infinite time to write down – then again, maybe that's just nonsensical).
I appreciate your patience and your explanations
---
On topic again: I just stumbled upon Cantor's theorem, which seems to be pretty much all you need to show that the set of all subsets of N is not countable. Here's my rephrasing it for the given problem (the actual theorem shows that any set has as a strictly lesser cardinality then its power set):
Let's assume that we can count P(N), the set of all subsets of N. This would mean that we have a bijective map f : N → P(N), i.e. a map f that provides a one-to-one correspondence between N and P(N).
P(N) contains at least as many elements as N, because for any n ∈ N, P(N) contains the set {n}. So, constructing an injective map is quite easy.
However, we get a problem with surjectivity, i.e. f cannot map to ALL elements in P(N). Here's why it doesn't work:
Let's examine one particular subset of N, that is to say
M = {n ∈ N | n ∉ f(n)},or verbally, the set of natural numbers that are not contained in the set that f maps them to. This particular subset of N will give us the desired contradiction. Here's how:
M is clearly in P(N) (since it's a subset of N) and because we require that f maps to ALL elements of P(N), there must be some m ∈ N so that f(m) = M.
Given any n ∈ N, is it in f(m) = M? Answer:
n ∈ f(m) ⇔ n ∈ M ⇔ n ∉ f(n).Now, what if n = m? Answer (just replace all n with m):
m ∈ f(m) ⇔ m ∈ M ⇔ m ∉ f(m).So, ultimately we have:
m ∈ f(m) ⇔ m ∉ f(m).
This, of course, is a contradiction, therefore our assumption must have been wrong and there is no such map f that provides a one-to-one correspondence between N and P(N). It follows that you cannot count P(N), the set of all subsets of N.Last edited by illidan; 08-15-2010 at 02:27 PM.

-
08-15-2010 05:38 PM #24Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Hmm, I think being a computer scientist may have given you a strange slant on this.
I don't see why checking if a point is in a disc is something you'd even want to do... we're talking about infinite sets here so computability doesn't really come into it. When I visualise counting discs, I just think about running through N, hence running through Q^2, and hence hitting every disc in finite time.
The formal proof would go something like...
Construct a function from N to Q^2 [previously justified]. Due to the density of Q, we can always find a point in Q^2 inside any given disc. Hence we have a function that assigns some n to each disc.
Note that it is not, as you said (I imagine you said it offhandedly), actually necessary to show that each disc has a unique n (in other words to show injectivity); in fact, with my mapping, it's pretty much as uninjective as can be; each disc has infinite elements in N which map to it.
However, what we have done is shown that the discs will fit inside N; if the collection of discs is infinite, it also follows that the size of the set of discs is the same as the size of the set of N (as there is no infinity less than the size of N). You don't need to create a bijection.
I wouldn't say that an infinite set is not well-defined. All that was required for the question was to know that these discs existed. I have an inkling that this may be related to the axiom of choice, but I haven't really studied that formally yet. The point is, there's really no problem in assuming that 'somebody' has created an infinite 'list' of discs. They might have used some kind of rule (like the Apollonian gasket) or have done it 'randomly', it's inconsequential.
Again I think we're probably weirded out by each other's differences here due to our subtle conditioning by our different educations. You're always concerned with whether you can practically do something or not, but I guess in maths we create infinite objects all the time without worrying, where a computer scientist would probably say 'wurgh!' or something similar.
I think most of what PS has said is correct (except the thing about his room mate's 'objection' to Cantor's work, which was less of an objection and more just completely ignoring it).
Your proof for the uncountability of P(N) is perfect. It's essentially the diagonal slash method; create an object which differs from the nth listed object by something with something 'n'ish about it.Last edited by Xei; 08-15-2010 at 05:43 PM.
-
08-15-2010 06:07 PM #25Much clear than mine. Other than bringing 'time' into it of course. This is math not physics
 Originally Posted by Xei;1518637s
Originally Posted by Xei;1518637s

No, that was correct. My room mate did in fact say that. In fact we almost came to blows over it a few times. If there's something that's not correct, please call me out on it. I am a little rusty. Originally Posted by Xei;1518637s
Originally Posted by Xei;1518637s
Last edited by PhilosopherStoned; 08-15-2010 at 06:22 PM.
Previously PhilosopherStoned
Similar Threads
-
What kinds of reality checks do you do?
By APSJ in forum Attaining LucidityReplies: 4Last Post: 06-02-2010, 05:05 AM -
Visions from all kinds of faiths
By Idolfan in forum Religion/SpiritualityReplies: 11Last Post: 06-16-2009, 01:47 AM -
Two kinds of dreams?
By Blink in forum Introduction ZoneReplies: 9Last Post: 11-08-2008, 12:05 AM -
My Theory On 2 Kinds Of Dreamers
By dylanshmai in forum General Lucid DiscussionReplies: 10Last Post: 07-12-2008, 09:57 AM -
Different Kinds Of Love
By Rav1 in forum PhilosophyReplies: 14Last Post: 10-29-2006, 05:52 PM




 6Likes
6Likes LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks




 Reply With Quote
Reply With Quote




Bookmarks