Sure is meta in here. |
|
Results 1 to 13 of 13
 7Likes
7Likes
Thread: Vague Thread Title
-
10-15-2012 05:22 AM #1D.V. Editor-in-Chief


- Join Date
- Jun 2006
- LD Count
- Lucid Now
- Gender
- Location
- 3D
- Posts
- 8,263
- Likes
- 4139
- DJ Entries
- 11
Vague Thread Title
I believe something because there is a lot of evidence to support it. For instance, if we compare it to a related subject which we can all agree is obviously true, refuting it becomes hypocritical. Furthermore, most of the research on the subject leads one to this conclusion. The only reason you may disagree with it is because you are still trapped in the old paradigm and are not giving the subject enough thought.
What say you?Last edited by Original Poster; 10-15-2012 at 05:30 AM.
Everything works out in the end, sometimes even badly.

-
10-15-2012 12:20 PM #2

---------
Lost count of how many lucid dreams I've had
---------
-
10-15-2012 10:35 PM #3Dionysian



- Join Date
- Jun 2010
- LD Count
- About 1 a week
- Gender

- Location
- Cirith Ungol
- Posts
- 895
- Likes
- 482
- DJ Entries
- 3
This is a rather vague subject matter to match the title but Ill give it a shot, of course correct me if I am missing your point (maybe if you provide an example I could have something tangible to work with). Paradoxically the degree of belief you have in a proposition being true is decreased the more empirical evidence there is to support it. Popper articulated this more eloquently than me "The probability of a theory is inversely proportional to its empirical content". What I take it that he means is that the more specific the theory or hypothesis describes some empirical state of affairs the less likely that theory is to be correct, again this seems counter intuitive but it can be expressed formally which might shed some light on the matter (or it might have the opposite effect, its been awhile since Ive thought about this stuff).
Take this classic example:
Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.
Given this back ground information which is more probable?
a) Linda is a bank teller.
b) Linda is a bank teller and active in the feminist movement.
Now 85% of people think that "b" is more likely than "a" but this is incorrect and we can see why by consulting a universal law of probability theory:
P(A) ≥ P(A & B)
if you are not familiar with probability theory this basically means "the probability of A is more likely than the probability of A and B" this is why extremely general propositions like "the world exists" (a tautology) have a probability of .9 or 1 and it would be absurd to believe the converse of the proposition, it has such a high degree of certain it is obviously true. So the more specific a theory gets the less likely it is to be true and the more general a theory is the more likely it is to be true, yet general theories explain nothing and the complexity of the world requires specific theories paradoxically.
Just to nitpick a little bit
Because scientific inquiry relies on probability theory to such a large degree this is not always the case, sometimes more research just narrows down the number of possible conclusions but never really comes to a certain conclusion. Think about the white swan induction problem; we can never really prove that all swans are white but we can disprove it with one single empirical observation. In a sense testing a hypothesis just informs us what is more likely not to be true than what is actually true but of course this process of elimination only serves to get us closer to the "capital T" truth. Anyway Ive rambled long enough, what say you?Last edited by stormcrow; 10-15-2012 at 10:41 PM.
-
10-15-2012 11:01 PM #4Dionysian



- Join Date
- Jun 2010
- LD Count
- About 1 a week
- Gender

- Location
- Cirith Ungol
- Posts
- 895
- Likes
- 482
- DJ Entries
- 3
-
10-15-2012 11:07 PM #5
-
10-15-2012 11:13 PM #6Dionysian



- Join Date
- Jun 2010
- LD Count
- About 1 a week
- Gender

- Location
- Cirith Ungol
- Posts
- 895
- Likes
- 482
- DJ Entries
- 3
-
10-16-2012 01:03 AM #7
Is Original Poster Omnis? I've been gone for a while...
This is funny:
1) OP makes a vague meta-ish thread
2) marvo makes a meta remark about the meta-ish thread
3) Stormcrow makes a meta remark about Marvo's remark
4) Stormcrow makes a meta remark about the fact that he's being meta too
5) I'm writing this list making meta observations about it all
Are you basically just urging people to accept evidence? It seems there must be some specific issue that provoked you to start this thread, so please share it if there is.
Never heard this before so I'm glad you brought it up. It makes sense for cases in which experimentation only narrows down the possibilities. But P(A & B) would be greater than P(A) in cases where the A in P(A & B) has a lot more evidence to support it. For example, before any experiments P(A) might be 0.2. And then experiments are conducted to learn more about it and it turns out that "A [implies] B" must be true as well. If that were the only thing concluded then A would now be less likely, which is what I think you're saying. But if so much evidence is found that P(A) is now 0.9, P(A & B) is probably going to be greater than P(A) was before the experiments. Since this is generally what happens (I think) then your criticism might only be a minor consideration.Last edited by Dianeva; 10-16-2012 at 01:06 AM.
-
10-16-2012 01:40 AM #8D.V. Editor-in-Chief


- Join Date
- Jun 2006
- LD Count
- Lucid Now
- Gender
- Location
- 3D
- Posts
- 8,263
- Likes
- 4139
- DJ Entries
- 11
To me it comes down to validation vs falsification. But stormcrow also brought up linguistic problems with arguments. The moment you open your mouth, you are wrong. Attempting to condense the many facets of life into specific categories with specific meanings may be useful for communication but it's important to look beyond the communication itself. If you agree with someone's point, the way they explain their point is mostly irrelevant except as a bridge for them to understand how you would explain the point.
This also comes down to experiential and conceptual knowledge. Conceptual factors in probability cannot agree with the complexity of experiential factors. If you give someone a word problem such as attempting to describe who Linda is, conceptual factors are limited to the factors you describe in the problem. We are therefore no longer actually talking about Linda, we are transposing Linda into a model and are therefore only able to assess probability on the model and not the person.
This is where validation can become an obstacle, and a pitfall for objectionists. It's important not to confuse what you have been led to believe with what is true. Beliefs serve action, and in fact the word belief can serve communication when used tenuously.
Everything works out in the end, sometimes even badly.

-
10-16-2012 09:19 PM #9Dionysian



- Join Date
- Jun 2010
- LD Count
- About 1 a week
- Gender

- Location
- Cirith Ungol
- Posts
- 895
- Likes
- 482
- DJ Entries
- 3
Hey Dianeva, as I mentioned previously this does seem very counter-intuitive so let me attempt to explain why P(A) < P(A & B) is a fallacy. The probability of a conjunction is never greater than the probability of the conjuncts respectively. Think about it like a venn diagram, the conjunction of two sets (Linda is a bank teller and active in the feminist movement) is always less than or equal to the probability of the conjuncts; to affirm the converse (P(A) < P(A & B) would violate Bayes rule which is the gold standard for rational decision-making. Now the probability of A might be strengthened in light of evidence B but the probability of the conjuncts A ∨ B (disjunction) is still greater than A ∧ B (the conjunction); in order to for the conjunction to be true both A&B must be true respectively but in order for the disjunction to be true either A or B must be true, if that makes any sense.
Human reasoning and decision-making is subject to a number of systematic errors and biases in part because we ordinarily rely on intuitive reasoning and the application of heuristics as opposed to applying the normative methods of reasoning (formal logic, probability theory). Because we are generally poor at reasoning with probabilities it is hard to spot the fallacies in our own judgments, think about the Monty Hall problem, it is infuriating at first because the conclusion seems utterly counter-intuitive yet when we apply Bayesian reasoning to the problem the answer becomes quite clear. I do think there was a thread about the Monty Hall problem at somewhere around here. Mathematically P(A) ≥ P(A & B) and P(B)≥ P(A & B) is a universal law, it is a necessary consequence of the axioms of probability theory, we have to assume them in order to reason probabilistically in the first place.Last edited by stormcrow; 10-16-2012 at 09:29 PM.
-
10-17-2012 05:07 AM #10
Thanks and I will look up the Money Hall problem (never heard of it before), but I think I was a bit unclear in what I was saying. It seemed pretty intuitive to answer (a) to your example, I get the logic and wasn't arguing that P(A) can be < P(A & B). Only that it doesn't really apply to experimental cases, which is what you brought it up for in the first place. For it to work, it's assumed that P(A) is held constant, both while evaluating P(A) and while evaluating P(A & B). But in cases of experiments, P(A) might first be a small value and then afterwards be a large value. So you might as well be saying P(A1) < P(A2 & B), which there would be no problem with.
Not intending to sound offended if I do just don't want you to think I'm stupid
EDIT: Looked up the Money Hall problem and actually have heard it before just didn't know it was called that. And that is extremely unintuitive. After much effort and frustration I finally understood it once but now I don't remember why. *frustrated*Last edited by Dianeva; 10-17-2012 at 05:10 AM.
-
10-18-2012 06:30 AM #11
-
10-28-2012 04:29 AM #12You are dreaming right now.
-
10-28-2012 02:59 PM #13Banned


- Join Date
- Aug 2005
- Posts
- 9,984
- Likes
- 3084
Dianeva and stormcrow; it looks like you're talking past each other. There are two different concepts.
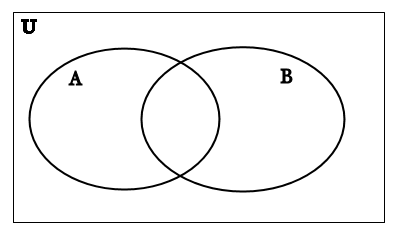
The probability of X, for instance X = "throwing two coins and getting a head and a tail", basically just means look at all possible events (the 'event space'), for instance "heads heads, heads tail, tail heads, tail tail", and take the ratio of the number of those events which are correctly described by X, for instance "heads tail, tail heads", to the total number of possible events (regardless of X or not X), which in this example gives 1/2.
P(A & B) means the probability that both A and B occur. Obviously this will always be less than or equal to P(A) [or P(B)], because otherwise you'd be saying that more events could be described by 'A&B' than just 'A'; but obviously that's not true, because for A&B to be true, A must be true. That is to say, A&B is a subset of A, and so it's smaller. stormcrow's example about feminist bankers is a good one for this.
The source of confusion for these kind of things is usually that people have some vague and rather incorrect notions of what 'probability' means. In reality, it's just set theory. Stop thinking about uncertainty. We're just measuring sizes of sets. Therefore it's very useful to consider a Venn diagram, shown below. U represents all possible outcomes. A represents all outcomes which could be described by "A"; B likewise, and where these two coincide is "A&B". It's now easy to see that P(A&B), the ratio of the size of A&B to the size of U, will always be smaller than or equal to P(A), the ratio of the size of A to the size of U, because clearly A&B is smaller than A.
Now the second concept I mentioned. This is P(A|B), "the probability of A given B". This means that we take it as given that B has already occurred, and then ask what the probability of A would be in light of this. If again you look below, you should actually be able to derive a formula for this. We're taking B as true, so B, rather than U, is our set of possible events. We now want all instances described by A, in B. This is just P(A&B). So the conclusion is that the probability of A, given B, i.e. the ratio of the number of possible events where A occurred to the total number of possible events, given B, is just P(A&B)/P(B).
And if you play around with circles, you should find that you can indeed make P(A|B) take any possible value between 0 and 1, regardless of the size of P(A). Sometimes B makes A more likely (if A is positively linked with B somehow, for instance B = "it's raining", A = "you are sad"), sometimes B makes A less likely, and sometimes A is independent from B, i.e. the size of A in B relative to B is the same as the size of A relative to U (for instance, tossing two coins, and A = "the first is heads", B = "the second is heads").
Similar Threads
-
Hi (not a very exciting thread title)
By MastaBlasta in forum Introduction ZoneReplies: 1Last Post: 01-31-2011, 06:05 PM -
(Thread title for another R/S debate.)
By mini0991 in forum Senseless BanterReplies: 3Last Post: 11-16-2009, 05:40 PM -
Funny thread title pairs
By arby in forum The LoungeReplies: 72Last Post: 12-19-2008, 07:24 PM -
Possible...? <----(vague title)
By cooter in forum Introduction ZoneReplies: 2Last Post: 02-17-2005, 10:27 PM




 LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks



 Reply With Quote
Reply With Quote


Bookmarks